Devoir de maths corrigé, Exponentielle et suites numériques
Première générale, spécialité mathématiques
Devoir de mathématiques, et corrigé, sur les exponentielles et les suites, posé en spé maths, première générale, année scolaire 2023/2024
Exercice 1: Deux inéquations avec des exponentielles
Exercice 2: Variation d'une fonction produit et composée avec exponentielle
Étudier le sens de variation de la fonction 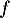 définie par
définie par
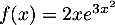 .
.
Préciser l'équation de la tangente au point d'abscisse 0.
On a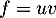 avec
avec 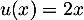 donc
donc 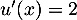 et
et 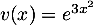 soit
soit 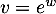 avec
avec
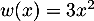 donc
donc 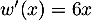 et alors
et alors 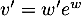 soit
soit 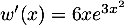 .
.
On a alors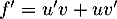 , soit
, soit
![\[f'(x)=2e^{3x^2}+2x\times 6xe^{3x^2}=\left( 12x^2+2\right) e^{3x^2}\]](/Generateur-Devoirs/1S/ChapExp/exvarpc_c/11.png)
On a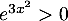 et le premier terme est du second degré de discriminant
et le premier terme est du second degré de discriminant 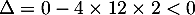 et n'admet donc aucune racine réelle.
et n'admet donc aucune racine réelle.
On a donc
![\[\begin{tabular}{|c|cccc|}\hline
$x$ & $-\infty$ && &$+\infty$ \\\hline
$12x^2+6$ && $+$ &&\\\hline
$e^x$ && $+$ &&\\\hline
$f'(x)$ && $+$ &&\\\hline
&&&&\\
$f$&&\Large{$\nearrow$}&&\\
&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exvarpc_c/14.png)
La tangente a pour équation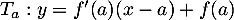 , soit avec
, soit avec  ,
,
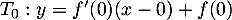 ,
donc ici, avec
,
donc ici, avec 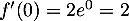 et
et 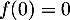 , on trouve l'équation
, on trouve l'équation
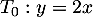
Cacher la correction
Préciser l'équation de la tangente au point d'abscisse 0.
Correction exercice 2
On a
On a alors
On a
On a donc
![\[\begin{tabular}{|c|cccc|}\hline
$x$ & $-\infty$ && &$+\infty$ \\\hline
$12x^2+6$ && $+$ &&\\\hline
$e^x$ && $+$ &&\\\hline
$f'(x)$ && $+$ &&\\\hline
&&&&\\
$f$&&\Large{$\nearrow$}&&\\
&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exvarpc_c/14.png)
La tangente a pour équation
Cacher la correction
Exercice 3: Suite récurrente, construction graphique des premiers termes
Soit 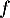 la fonction définie par
la fonction définie par 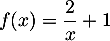 sur
sur ![$]0;+\infty[$](/Generateur-Devoirs/1S/Chap9/exrecgraph/3.png) .
.
On définit la suite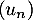 par
par 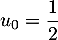 et, pour tout entier
et, pour tout entier 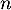 , par
, par 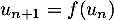 .
.
Cacher la correction
On définit la suite
- Calculer
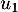 .
.
- Déterminer le sens de variation de
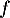 puis tracer l'allure de la courbe représentative de
puis tracer l'allure de la courbe représentative de 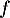 dans un repère.
dans un repère.
- Construire sur ce graphique les points
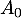 ,
, 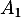 ,
, 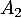 ,
, 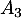 et
et 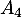 d'ordonnées nulles et d'absisses
d'ordonnées nulles et d'absisses 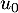 ,
, 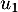 ,…,
,…,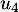 .
.
- Quelle conjecture peut-on faire quant-à la valeur limite de cette suite ? Calculer la valeur exacte de cette limite éventuelle.
Correction exercice 3
-
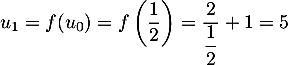 .
.
- On a
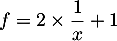 d'où
d'où 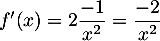 .
.
On trouve ainsi que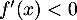 pour tout
pour tout ![$x\in]0;+\infty[$](/Generateur-Devoirs/1S/Chap9/exrecgraph_c/5.png) et donc que
et donc que 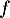 est strictement décroissante sur cete intervalle.
est strictement décroissante sur cete intervalle.
- On trace alors l'allure de la courbe et sur le graphique la droite d'équation
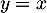 et on construit les points demandés sur l'axe des abscisses.
et on construit les points demandés sur l'axe des abscisses.
{\i}\psline(-.08,\i)(.05,\i)}
%\psplot{.1}{5}{2 x div 1 add}
% Definition de la fonction f de u_{n+1}=f(u_n)
\newcommand{\f}[1]{2 #1 div 1 add}
% Et son tracer:
\psplot[linewidth=1.4pt]{0.1}{7}{\f{x}}
% ainsi que le tracer de la droite y=x
\psplot{-.5}{6.5}{x}
% Defintion de la fonction it\'er\'ee:
% par ex.: fn{3}{x}=f(f(f(x)))
\newcommand\fn[2]{%
\ifnum#1=1
\f{#2}%
\else
\f{\fn{\numexpr#1-1}{#2}}%
\fi
}
% Valeur initiale (u_0)
\def\xinit{.5}
\def\nmax{4}
% Initialisation pour u_0
\psline[linestyle=dashed]
(\xinit,0)
(!\xinit\space\f{\xinit})
(!\f{\xinit}\space\f{\xinit})
\rput(\xinit,-0.3){$A_0$}
% Boucle pour u_1, u_2, ..., u_nmax
\multido{\i=1+1}{\nmax}{
\psline[linestyle=dashed]
(!\fn{\i}{\xinit} \space 0)
(!\fn{\i}{\xinit} \space \fn{\i}{\xinit})
(!\fn{\i}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
(!\fn{\numexpr\i+1}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
\rput(!\fn{\i}{\xinit}\space 0){$\tm$}
\rput(!\fn{\i}{\xinit}\space -0.3){$A_\i$}
}
\end{pspicture*}\]](/Generateur-Devoirs/1S/Chap9/exrecgraph_c/8.png)
- La suite semble tendre vers l'abscisse du point d'intersection entre la courbe de
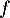 et la droite d'équation
et la droite d'équation 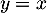 .
.
L'abscisse de ce point vérifie dont l'équation
![\[f(x)=x\iff\dfrac2x+1=x\]](/Generateur-Devoirs/1S/Chap9/exrecgraph_c/11.png)
soit, en multipliant par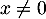 (car
(car 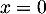 n'est pas solution),
n'est pas solution),
![\[2+x=x^2\iff x^2-x-2=0\]](/Generateur-Devoirs/1S/Chap9/exrecgraph_c/14.png)
Cette équation du second degré a pour discriminant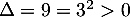 et admet donc deux solutions
et admet donc deux solutions 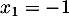 et
et 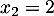 .
.
La première solution n'est pas celle recherchée, et la seule limite éventuelle est donc
n'est pas celle recherchée, et la seule limite éventuelle est donc 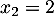 .
.
Cacher la correction
Exercice 4: Sens de variation d'une suite
On considère la suite 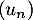 définie par
définie par 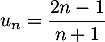 .
.
On considère la suite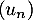 définie par
définie par 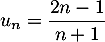 .
.
Cacher la correction
- Calculer les premiers termes
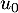 ,
, 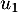 et
et 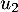 .
.
- Déterminer, pour tout entier
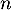 , le signe de
, le signe de 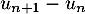 .
.
Donner alors le sens de variation de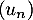 .
.
Correction exercice 4
On considère la suite
-
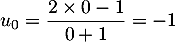 ;
;
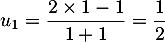 ;
;
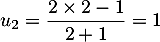
- Pour tout entier
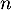 ,
,
![\[\begin{array}{ll}
u_{n+1}-u_n&=\dfrac{2(n+1)-1}{(n+1)+1}-\dfrac{2n-1}{n+1}\\[1em]
&=\dfrac{2n+1)}{n+2}-\dfrac{2n-1}{n+1}\\[1em]
&=\dfrac{(2n+1)(n+1)-(2n-1)(n+2)}{(n+2)(n+1)}\\[1em]
&=\dfrac{3}{(n+2)(n+1)}
\enar\]](/Generateur-Devoirs/1S/Chap9/exvar0_c/7.png)
Comme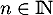 , on a en particulier
, on a en particulier 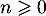 et donc
et donc 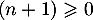 et
et 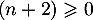 .
.
En particulier, on a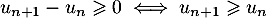 ce qui montre que la suite
ce qui montre que la suite 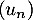 est croissante.
est croissante.
Cacher la correction
Quelques autres devoirs
Probabilités conditionnelles et calculs de probabilités avec un arbre de probabilités. Propriétés algébriques de l'exponentielle et une étude de fonctionDevoir: Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
étude de fonctions avec exponentielle, calculs de dérivées, et position relative d'une courbe et d'une droite
étude de fonctions avec exponentielle, premier devoir sur les suites: calcul des premiers termes et sens de variation, construction des premiers termes d'une suite
dérivée et sens de variation d'une fonction rationnelle - Calculs algébriques et équations avec exponentielles - Probabilités conditionnelles et arbre de probabilité
équations et inéquations avec exponentielles, variation de fonctions avec exponentielle, probabilités conditionnelle et arbre de probabilité
Quelques exercices corrigés
Exercices corrigés
Construction des premiers termes d'une suite récurrente
Exercices corrigés
Suite récurrente, construction graphique des premiers termes
Exercices corrigés
Suite récurrente avec exponentielle, construction graphique des premiers termes
Exercices corrigés
Sens de variation d'une suite homographique
Exercices corrigés
Calcul des premieres termes et variation d'une suite récurrente
Voir aussi: