Pente en pourcentage et degrés

En géométrie, on mesure les angles en degrés ou en radians. Des calculs de longueurs, de hauteurs, peuvent se faire en utilisant la trigonométrie.
En topographie, où on cherche à représenter sur carte les reliefs, terrains, bâtiments, maisons, routes, …), ces angles ou pentes sont exprimés en pourcentage.
La signalisation routière utilise aussi des angles exprimés en pourcentage
Panneau de signalisation routière: pente de 10%

Convertisseur angle / pente

La calculatrice suivante permet de convertir automatiquement entre un angle exprimé en degré et la pente correspondante en pourcentage. Il suffit d'entrer une des deux valeurs et l'autre est calculée automatiquement.
Calculatrice de conversion
°
%

Deux valeurs particulières:
  • Avec une pente de 10%, le dénivelé est de un dixième de la distance horizontale parcourue: si on parcourt 100 mètres, on monte (ou descend) de 10 mètres.
  • Une pente de 100% est bien possible: le dénivelé est égal à la distance horizontale parcourue: si on parcourt 100 mètres, on monte (ou descend) aussi de 10 mètres; l'angle correspondant est donc de 45°

Tableau de correspondance entre degrés et pourcentages de pente

Le tableau suivant donne quelques repères de correspondance rapide entre la valeur de l'angle en degrés et le pourcentage de pente.
degrés% de penteDénivelé
5°9% dénivelé de 9 cm pour 1 mètre horizontal
10°18% dénivelé de 18 cm pour 1 mètre horizontal
19°35% dénivelé de 35 cm pour 1 mètre horizontal
26,5°50% dénivelé de 50 cm pour 1 mètre horizontal
30°58% dénivelé de 58 cm pour 1 mètre horizontal
45°100% dénivelé de 1 mètre pour 1 mètre horizontal

Pente d'un toit - Hauteur du pignon

Quelle est la hauteur du pignon selon sa alargeur et la pente du toit ? La calculatrice suivante calcule automatiquement la correspondance entre la pente du toit en pourcentage, l'angle en degré, et la hauteur du pignon sous le faîtage en fonction de la longueur horizontale.
Les résultats des calculs sont arrondis au dixième près.
La pente que l'on peut donner à un toit dépend de plusieurs paramètres: des contraintes locales (esthétique, urbanisme), contraintes mécaniques selon la région (résistance à la neige, aux vents, ...). Les normes techniques sont édictées par le DTU

Longueur de la pente

On peut s'intéresser aussi à la longueur de la pente, ou longueur de la descente en fonction de la pente en pourcentage, de l'angle en degré, ou encore de la hauteur. Ce calcul peut donner la distance réelle parcourue en suivant la pente, ou encore pour la longueur de la pente d'un toit de maison et donc le nombre de tuiles à prévoir.


Quelques rappels de trigonométrie

Dans un triangle rectangle,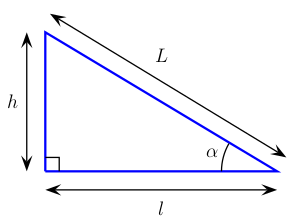
Trigonométrie dans un triangle rectangle
on peut calculer les longueurs et angles à en utilisant les relations trignométriques:
  • le cosinus:
    cos(α) = l/L
  • le sinus
    sin(α) = h/L
  • et enfin la tangente
    tan(α) = h/l
    Cette Dernière relation est directement aussi la définition de la pente, en pourcentage,
    pente = h/l = tan(α)
On peut enfin calculer la longueur de la pente en utilisant au choix le sinus ou le cosinus:
L = l/cos(α) = h/sin(α)
On peut bien sûr aussi utiliser, comme on parle d'un triangle rectangle, du théorème de Pythagore:
L2 = h2 + l2
soit
L = h2 + l2


Voir aussi:
LongPage: h2: 4 - h3: 1