Devoir de maths corrigé, Probabilités conditionnelles et exponentielle
Première générale, spécialité mathématiques
Devoir de mathématiques, et corrigé, sur le produit scalaire et les probabilités conditionnelles et arbre de probabilités. Devoir posé en spé maths, première générale, année scolaire 2024/2025
Exercice 1: Arbre de probabilité et probabilités conditionnelles
Pour préparer l'examen du permis de conduire, on distingue deux types de formation :
On considère un groupe de 300 personnes venant de réussir l’examen du permis de conduire. Dans ce groupe :
On interroge au hasard une personne du groupe considéré, et on considère les évènements suivants :
Cacher la correction
- la formation avec conduite accompagnée ;
- la formation traditionnelle.
On considère un groupe de 300 personnes venant de réussir l’examen du permis de conduire. Dans ce groupe :
- 75 personnes ont suivi une formation avec conduite accompagnée ; parmi elles, 50 ont réussi l’examen à leur première présentation et les autres ont réussi à leur deuxième présentation.
- 225 personnes se sont présentées à l’examen suite à une formation traditionnelle ; parmi elles, 100 ont réussi l’examen à la première présentation, 75 à la deuxième et 50 à la troisième présentation.
On interroge au hasard une personne du groupe considéré, et on considère les évènements suivants :
-
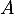 : « la personne a suivi une formation avec conduite accompagnée » ;
: « la personne a suivi une formation avec conduite accompagnée » ;
-
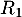 : « la personne a réussi l’examen à la première présentation » ;
: « la personne a réussi l’examen à la première présentation » ;
-
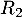 : « la personne a réussi l’examen à la deuxième présentation » ;
: « la personne a réussi l’examen à la deuxième présentation » ;
-
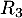 : « la personne a réussi l’examen à la troisième présentation ».
: « la personne a réussi l’examen à la troisième présentation ».
- Modéliser la situation par un arbre pondéré.
- Calculer la probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l’examen à sa deuxième présentation.
- Quelle est la probabilité que la personne interrogée ait réussi l’examen à sa deuxième présentation.
- La personne interrogée a réussi l’examen à sa deuxième présentation. Quelle est la probabilité qu’elle ait suivi une formation avec conduite accompagnée?
Correction exercice 1
- On modélise la situation par un arbre pondéré.
{.3}\rput(3.3,1.6){$\frac{25}{75}$}
\rput(4.3,.5){$R_3$}\rput(3.3,.7){$0$}
%
\psline(2.5,-1.5)(4,-1.5)
\psline(4,-.5)(2.5,-1.5)(4,-2.5)
\rput(4.3,-.5){$R_1$}\rput(3.3,-.5){$\frac{100}{225}$}
\rput(4.3,-1.5){$R_2$}\pscircle[linestyle=none,fillstyle=solid,fillcolor=white](3.3,-1.6){.3}\rput(3.3,-1.5){$\frac{75}{225}$}
\rput(4.3,-2.5){$R_3$}\rput(3.3,-2.4){$\frac{50}{225}$}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap7/exCAPC_c/1.png)
- La probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l'examen à sa deuxième présentation est:
![\[\begin{array}{ll}P\left( A\cap R_2\rp&= P(A)\times P_{A}\left( R_2\rp\\[.3em]
&=\dfrac{75}{300}\tm\dfrac{25}{75}=\dfrac{1}{12}\enar\]](/Generateur-Devoirs/1S/Chap7/exCAPC_c/2.png)
- La probabilité que la personne interrogée ait réussi l'examen à sa deuxième présentation est
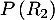 soit, d'après la formule des probabilités totales,
soit, d'après la formule des probabilités totales,
![\[\begin{array}{ll}
P\left( R_2\right) %&= P\left( A\cap R_2\right) + P\left(\overline{A}\cap R_2\right)\\
&=P(A\cap R_2)+P(\overline{A}\cap R_2)\\[.5em]
&=\dfrac{75}{300}\tm\dfrac{25}{75}
+\dfrac{225}{300}\tm\dfrac{75}{225}\\[1em]
&=\dfrac{25}{300} + \dfrac{75}{300}
=\dfrac{100}{300}=\dfrac13\enar\]](/Generateur-Devoirs/1S/Chap7/exCAPC_c/4.png)
- La personne interrogée a réussi l'examen à sa deuxième présentation. La probabilité qu'elle ait suivi une formation avec conduite accompagnée est alors la probabilité conditionnelle:
![\[P_{R_2}(A) = \dfrac{P(A\cap R_2)}{P(R_2)}= \dfrac{\dfrac1{12}}{\dfrac13} = \dfrac3{12}=\dfrac14
\]](/Generateur-Devoirs/1S/Chap7/exCAPC_c/5.png)
Cacher la correction
Exercice 2: Courbe et tangentes de l'exponentielle
On considère la fonction exponentielle 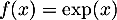 , définie sur
, définie sur 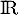 .
.
Donner les équations des tangentes à sa courbe au point d'abscisse 0 puis au point d'abscisse 1.
Tracer ces tangentes dans un repère ainsi que l'allure de la courbe de la fonction exponentielle.
L'équation de la tangente à la courbe de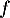 au point d'abscisse
au point d'abscisse 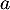 est
est
![\[T_a: y=f'(a)(x-a)+f(a)\]](/Generateur-Devoirs/1S/ChapExp/extgtexp_c/3.png)
et ainsi, en 0,
![\[T_0: y=f'(0)(x-0)+f(0)\]](/Generateur-Devoirs/1S/ChapExp/extgtexp_c/4.png)
avec, pour la fonction exponentielle,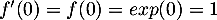 , d'où l'équation de la tangente
, d'où l'équation de la tangente
![\[T_0: y=1(x-0)+1=x+1\]](/Generateur-Devoirs/1S/ChapExp/extgtexp_c/6.png)
De même, au point d'abscisse 1,
![\[T_1: y=f'(1)(x-1)+f(1)\]](/Generateur-Devoirs/1S/ChapExp/extgtexp_c/7.png)
avec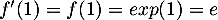 et donc
et donc
![\[T_1: y=e(x-1)+e=x\]](/Generateur-Devoirs/1S/ChapExp/extgtexp_c/9.png)
On trace alors ces deux tangentes et la courbe de l'exponentielle:
![\[\psset{unit=1.2cm}\begin{pspicture*}(-3,-1)(3,5.5)
\psline[arrowsize=8pt]{->}(-3,0)(3,0)\psline[arrowsize=8pt]{->}(0,-1)(0,5.5)
\psplot[linecolor=blue,linewidth=1.5pt]{-3}{2}{2.718 x exp}
\rput[r](-.1,1.1){1}
\psline[linestyle=dotted](1,0)(1,2.718)(0,2.718)
\rput[r](-.1,2.7){$e$}\rput(1,-.2){1}
\psplot{-3}{3}{x 1 add}\rput(-1.9,-.5){$T_0$}
\psplot{-3}{3}{2.718 x mul}\rput(-.5,-.5){$T_1$}
\end{pspicture*}\]](/Generateur-Devoirs/1S/ChapExp/extgtexp_c/10.png)
Cacher la correction
Donner les équations des tangentes à sa courbe au point d'abscisse 0 puis au point d'abscisse 1.
Tracer ces tangentes dans un repère ainsi que l'allure de la courbe de la fonction exponentielle.
Correction exercice 2
L'équation de la tangente à la courbe de
et ainsi, en 0,
avec, pour la fonction exponentielle,
De même, au point d'abscisse 1,
avec
On trace alors ces deux tangentes et la courbe de l'exponentielle:
![\[\psset{unit=1.2cm}\begin{pspicture*}(-3,-1)(3,5.5)
\psline[arrowsize=8pt]{->}(-3,0)(3,0)\psline[arrowsize=8pt]{->}(0,-1)(0,5.5)
\psplot[linecolor=blue,linewidth=1.5pt]{-3}{2}{2.718 x exp}
\rput[r](-.1,1.1){1}
\psline[linestyle=dotted](1,0)(1,2.718)(0,2.718)
\rput[r](-.1,2.7){$e$}\rput(1,-.2){1}
\psplot{-3}{3}{x 1 add}\rput(-1.9,-.5){$T_0$}
\psplot{-3}{3}{2.718 x mul}\rput(-.5,-.5){$T_1$}
\end{pspicture*}\]](/Generateur-Devoirs/1S/ChapExp/extgtexp_c/10.png)
Cacher la correction
Exercice 3: Simplifier les expressions avec exponentielles
Exercice 4: Équations et inéquations avec exponentielles
Exercice 5: Sens de variation d'une fonction
Déterminer le sens de variation de la fonction 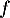 définie par l'expression
définie par l'expression
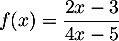 .
.
On fait attention à l'ensemble de définition de cette fonction: ici la fonction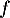 est définie lorsque
est définie lorsque 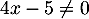 donc pour tout réel
donc pour tout réel 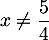 .
Son sens de variation est donné par le signe de sa dérivée.
.
Son sens de variation est donné par le signe de sa dérivée.
On a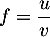 avec
avec 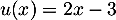 donc
donc 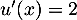 ,
et
,
et 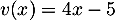 donc
donc 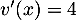 et alors
et alors
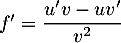 soit
soit
![\[\begin{array}{ll}f'(x)&=\dfrac{2(4x-5)-(2x-3)4}{(4x-5)^2}\\
&=\dfrac2{(4x-5)^2}
\enar\]](/Generateur-Devoirs/1S/Chap3/exhmg_c/10.png)
Comme pour tout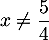 on a
on a 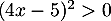 , on en déduit que
, on en déduit que 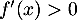 et donc que
et donc que 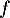 est strictement croissante sur
est strictement croissante sur 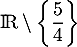 :
:
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $-\infty$ && $5/4$ && $+\infty$ \\\hline
$f'(x)$ & &$+$ && $+$ &\\\hline
&&&\psline(0,-1.25)(0,.9)\,\psline(0,-1.25)(0,.9)&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\nearrow$}&\\
&&&&&\\\hline\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exhmg_c/16.png)
Cacher la correction
Correction exercice 5
On fait attention à l'ensemble de définition de cette fonction: ici la fonction
On a
![\[\begin{array}{ll}f'(x)&=\dfrac{2(4x-5)-(2x-3)4}{(4x-5)^2}\\
&=\dfrac2{(4x-5)^2}
\enar\]](/Generateur-Devoirs/1S/Chap3/exhmg_c/10.png)
Comme pour tout
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $-\infty$ && $5/4$ && $+\infty$ \\\hline
$f'(x)$ & &$+$ && $+$ &\\\hline
&&&\psline(0,-1.25)(0,.9)\,\psline(0,-1.25)(0,.9)&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\nearrow$}&\\
&&&&&\\\hline\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exhmg_c/16.png)
Cacher la correction
Quelques autres devoirs
Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
Probabilités conditionnelles et calculs de probabilités avec un arbre de probabilités. Propriétés algébriques de l'exponentielle et une étude de fonctionDevoir: Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
étude de fonctions avec exponentielle, calculs de dérivées, et position relative d'une courbe et d'une droite
étude de fonctions avec exponentielle, premier devoir sur les suites: calcul des premiers termes et sens de variation, construction des premiers termes d'une suite
une étude des variations d'une fonction - Calcul de la valeur approchée d'un angle avec le produit scalaire dans un repère - Probabilités conditionnelles et réunion / intersection d'événements
Quelques exercices corrigés
Exercices corrigés
Réunion, intersection et incompatibilité
Exercices corrigés
Réunion, intersection et contraire
Exercices corrigés
Réunion et intersection, cartes à puces avec deux défauts
Exercices corrigés
Gâteaux à la crème et aux fruits
Exercices corrigés
Efficacité de stages de révision dans une université
Voir aussi: