Suites numériques - Cours et exercices corrigés

Première générale, spécialité maths

Exercice 1: Rappels, échauffement …
  1. Déterminer, en fonction de n, le signe de a(n) = 2n2+3n−5, b(n)=(6−n)(n2−6n+5), et c(n)=2n−6/n2−6n+5
    Correction
      La 1ère expression a(n) est une expression du second degré dont on détermine les deux racines 1 et −5/2 (avec le discriminant Δ ou une racine évidente) et dont on connaît alors le signe.
      n −∞ −52 1 +∞
      a(n) + 0 − 0 +


      La 2ème expression est un produit dont un des facteurs est un trinôme du second degré dont on détermine les deux racines 1 et 3 (avec le discriminant Δ ou racine évidente) et dont on connaît alors le signe. On peut alors dresser le tableau de signes du quotient
      n −∞ 1 5 6 +∞
      6−n + | + | + 0 −
      2n2 −6n + 5 + 0 − 0 + | +
      b(n) + 0 − 0 + 0 −


      Pour la 3ème expression c(n), le dénominateur est le trinôme du second degré de l'expression précédente.
      On peut alors dresser le tableau de signes du quotient
      n −∞ 1 3 5 +∞
      2n − 6 − | − 0 + | +
      2n2 −6n + 5 + 0 − | − 0 +
      c(n) − || + 0 − || +
  2. Soit f(x)=x2−3x+1.
    Pour un entier n quelconque, exprimer f(n+1)−f(n) puis donner le signe de cette expression en fonction de n.

    Correction
    On développe l'identité remarquable
    f(n+1) = (n+1)2−3(n+1)+1
    puis on développe et ordonne
    f(n+1) = n2−n−1
    puis on soustrait
    f(n+1) − f(n) = (n2−n−1) − (n2−3n+1)
    ce qui donne
    f(n+1) − f(n) = 2n−2

    On a alors le signe de cette expression du 1er degré (ou affine)
    n −∞ 1 +∞
    f(n+1) − f(n) − 0 +
  3. On considère l'expression un = n−1/n+2
    Exprimer un+1−un puis donner le signe de cette expression en fonction de n.

    Correction
    On exprime
    un+1 = (n+1)−1/(n+1)+2
    soit
    un+1 = n/n+3
    et donc
    un+1 − un = n/n+3 − n−1/n+2
    soit aussi, sur le même dénominateur
    un+1 − un = 3/(n+3)(n+2)
    On peut alors donner le tableau de signes:
    n −∞ −3 −2 +∞
    3 + | + | +
    n+3 − 0 + | +
    n+2 − | − 0 +
    un+1−un + || − || +
  4. Simplifier les expressions suivantes: 2n×2n+1 , 32(n+1)/3n , 1/3(3n)2 , 1/2 2/5 n 5n+1/2n−2
    On revoit ici les règles de calcul sur les puissances:
    2n×2n+1 =2n+n+1 = 22n+1
    32(n+1)/3n = 32(n+1)−n = 3n+2
    1/3(3n)2 = 3−1×32n = 32n−1
    1/2 2/5n 5n+1/2n−2 = 2−1 2n/5n 5n+1/2n−2 = 2−1+n−(n−2) 5n+1−n = 21 51 = 10
  5. Revoir aussi le calcul de dérivées et sens de variation des fonctions.


Définition d'une suite numérique

Définition:
Une suite est une fonction u de N dans R,
u: n ↦ u(n)
On note en général un le terme d'indice n au lieu de u(n), et la suite (un) au lieu de u.
un est un nombre de la suite, et (un) désigne l'ensemble de tous les nombres de la~suite.
Exemples: Soit (un) la suite définie par un = 2n−3, alors
  • u0=2×0−3=−3,
  • u1 = 2×1−3=−1,
  • u2=1,
  • u3=3, …
puis encore, par exemple,
  • u20=2×20−3=37,
  • u50=2×50−3=97,
  • u5250=2×5250−3=10497, …

Une suite numérique est une suite de nombres. On peut définir une suite de deux manières:
  • soit explicitement, avec une formule comme dans l'exemple précédent,
  • soit par récurrence, ou implicitement: on définit les nombres de la suites de proche en proche.

Définition explicite

Dans l'exemple précédent, le terme général un est l'image de l'entier n par une fonction usuelle:
un = f(n)
où f est la fonction affine f : x ↦ 2x−3.

Autres exemples:
  • un = 2n2−3n+5; On a un = f(n) avec la fonction du second degré f : x ↦ 2x2−3x+
  • vn = 6n+3/n+1 ; On a vn = g(n) avec la fonction rationnelle g : x ↦ 6x+3/x+1
  • wn = 2n; On a wn = h(n) avec la fonction exponentielle h : x ↦ 2x

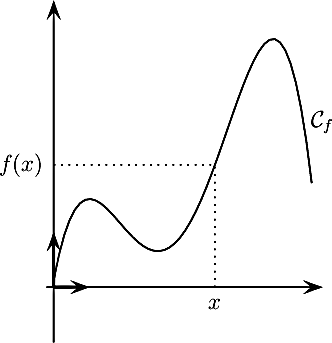
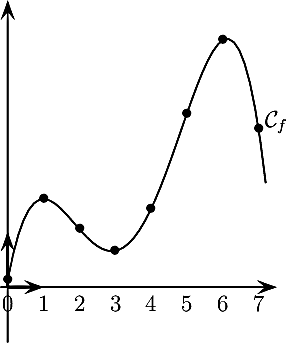
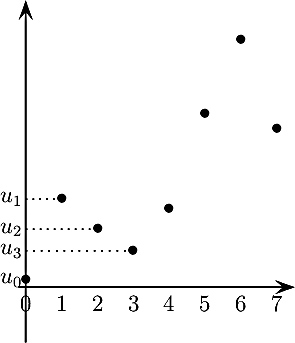
Remarque: on ne considère que les images de f pour des valeurs entières, et non pas pour tous les nombres réels d'un intervalle: on dit alors qu'on échantillonne, ou qu'on numérise, la fonction f.
Fonction et sa courbe
Courbe d'une fonction à échantilloner
Échantillonnage
Courbe échantillonnée
Échantillons / suite
Echantillons seuls de la courbe


Définition d'une suite par récurrence

On peut définir une suite en se donnant son premier terme u0 et une relation qui permet de calculer un terme de la suite à partir de son prédécesseur: on connaît u0, à partir duquel on peut calculer u1, à partir duquel on peut calculer u2, …
On calcule ainsi les termes au fur et à mesure, de proche en proche.

Exercice 2
On définit la suite (un) par son premier terme u0 = 1000 puis, pour tout entier n, par la relation un+1 = 1,04un.
Calculer u1, u2, u3, u10, u50.



Plus généralement, une suite est définie par récurrence par une relation de la forme
un+1 = f (un)
où f est une fonction définie, a priori, sur R.

Exercice 3
Pour chaque suite suivante définie par récurrence, calculer les quatre premiers termes de la suite:
  1. Suite (un) définie par u0 = 2 puis, pour tout entier n, par un+1 = 2un+3.

    On a
    • u0 = 2
    • u1 = 2u0+3 = 2×2+3 = 7
    • u2 = 2u1+3 = 2×7+3 = 17
    • u3 = 2u2+3 = 2×17+3 = 37
  2. Suite (vn) définie par v0 = 1 puis, pour tout entier n, par vn+1 = 1/vn+1.

    On a
    • v0 = 1
    • v1 = 1/v0+1 = 1/1+1 = 1/2
    • v2 = 1/v1+1 = 1/1/2+1 = 1/3/2 = 2/3
    • v3 = 1/v2+1 = 1/2/3+1 = 1/5/3 = 3/5
  3. Suite (wn) définie par w1 = 1 puis, pour tout entier n, par wn+1 = wn2+1.

    On a
    • w1 = 1
    • w2 = w12+1 = 12+1 = 2
    • w3 = w22+1 = 2+1 = 3
    • w4 = w32+1 = 3+1 = 2
  4. Suite (xn) définie par x1 = 0 puis, pour tout entier n, par xn+1 = xn2 + 1/2n+1.

    On a
    • x1 = 0
    • x2 = x12 + 1/2×1+1 = 02 + 1/3 = 1/3
    • x3 = x22 + 1/2×2+1 = 1/9 + 1/5 = 14/45
  5. Suite (zn) définie par z0 = 1 et z1 = 2 puis, pour tout entier n, par zn+2 = 2zn+1 + zn.

    On a
    • z0 = 1
    • z1 = 2
    • z2 = 2z1+z0 = 2×1+2 = 4
    • z3 = 2z2+z1 = 2×4+2 = 10


Exercice 4
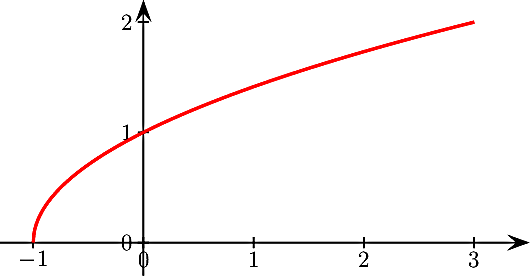
On donne la fonction f définie sur [−1; +∞[ par f(x) = x+1 et sa courbe représentée sur le graphique suivant.
On définit la suite (un) par son premier terme u0 = −0,8 et la relation de récurrence un+1 = un+1.
Placer u0 sur l'axe des abscisses, puis construire graphiquement les points d'abscisse u1, u2, … , u5.
(On pourra s'aider de la droite d'équation y=x)
Courbe de la fonction de récurrence


Voir aussi: Construction graphique des premiers termes d'une suite récurrente, pour des explications sur un exemple de la construction détaillée, étape par étape.

Exercice 5
Soit la fonction f définie sur R par l'expression f(x) = 1/2x+3
  1. On définie la suite (un) par u0 = 1 et un+1 = f (un).
    Calculer u1 et u2.
  2. Représenter graphiquement Cf et construire sur l'axe des abscisses de ce graphique les première valeurs u1 à u5.
  3. Quel semble être le sens de variation de la suite (un) ? Vers quelle valeur limite semble-t-elle tendre ?



Exercice 6
On considère la fonction f définie sur [0;+∞[ par
f(x) = 6 − 5/x+1
et la suite (un) telle que u0 = 0,5 et un+1 = f (un).
  1. Étudier le sens de variation de f.
  2. Tracer la courbe représentative de f dans un repère orthonormal d'unité graphique 2cm.
  3. Placer u0 sur l'axe des abscisses puis construire graphiquement sur l'axe des abscisses les premiers termes u1, u2, u3 et u4.
  4. Quel semble être le sens de variation de la suite (un) ? Vers quelle valeur limite semble-t-elle tendre ?



Exercice 7
On considère la fonction f définie sur [0;+∞[ par
f(x) = 1 + 5/x+1
et la suite (un) telle que u0 = 0,5 et un+1 = f (un).
  1. Étudier le sens de variation de f.
  2. Tracer la courbe représentative de f dans un repère orthonormal d'unité graphique 2cm.
  3. Placer u0 sur l'axe des abscisses puis construire graphiquement sur l'axe des abscisses les premiers termes u1, u2, u3 et u4.



Sens de variation d'une suite

Définition:
  • Une suite (un) est croissante si pour tout entier naturel n, on a un+1≥un.
  • Une suite (un) est décroissante si pour tout entier naturel n, on a un+1≤un.
  • Une suite (un) est décroissante si pour tout entier naturel n, on a un+1 = un.
  • Une suite croissante ou décroissante est dite monotone.
  • Une suite est strictement monotone, croissante ou décroissante, si les inégalités sont strictes: un+1< un ou un+1> un

Méthode: Étudier le sens de variation d'une suite (un) revient donc à comparer, pour tout entier n, les termes consécutifs un+1 et un, soit aussi à étudier le signe de la différence un+1 − un.

Exercice 8
Étudier le sens de variation des suites définies par les expressions:
  1. un = n2−n+2

    un+1 − un = ((n+1)2−(n+1)+2) − (n2−n+2)
    soit en développant
    un+1 − un = 2n
    et donc, pour tout entier naturel n on a
    un+1 − un = 2n ≥ 0
    ce qui montre que la suite est croissante.
  2. un = 2n/3n

    un+1 − un = 2n+1/3n+1 − 2n/3n
    soit en factorisant
    un+1 − un = 2n/3n 2/3 −1 = 2n/3n − 1/3 <0
    ce qui montre que la suite est strictement décroissante.
  3. un = 3n−2/n+1

    un+1 − un = 3(n+1)−2/(n+1)+1 − 3n−2/n+1 = 3n+1/n+2 − 3n−2/n+1
    soit aussi, sur le même dénominateur,
    un+1 − un = 5/(n+1)(n+2)
    Le dénominateur est positif (car n est un entier naturel, donc positif), et donc aussi
    un+1 − un>0
    ce qui montre que la suite est strictement croissante.
  4. un = 1/3n+3

    un+1 − un = 1/3(n+1)+3 − 1/3n+3 = 1/3>0
    ce qui montre que cette suite est strictement croissante.
  5. (un) définie par u0 = 2 et pour n≥1, un+1 = un−n

    On a directement, d'après la définition même de la suite
    un+1 − un = −n
    qui est négatif puisque n est un entier naturel (donc positif).
    Ainsi, cette suite est décroissante.
  6. un = (n−5)2

    un+1 − un = ((n+1)−5)2 − (n−5)2
    soit
    un+1 − un = (n−4)2 − (n−5)2 = 2n−9
    Comme n est un entier naturel, on a 2n−9≥0 dès que n≥5 et donc cette suite est décroissante pour n∈[0;4] et croissante pour n≥5.
  7. un = − 1/2 n

    un+1 − un = − 1/2 n+1 + 1/2 n
    soit en factorisant,
    un+1 − un = 1/2 n −1/2+1 = 1/2 n 1/2
    c'est-à-dire finalement
    un+1 − un = 1/2 n+1 >0
    et la suite est donc strictement croissante.
  8. un = 2n+2/3n

    un+1 − un = 2(n+1)+2/3n+1 − 2n+2/3n
    soit
    un+1 − un = 2n+3/3n+1 − 2n+2/3n
    et donc, en factorisant,
    un+1 − un = 2n+2/3n 2/3−1 = 2n+2/3n −1/3
    soit encore, finalement,
    un+1 − un = −2n+2/3n+1<0
    et la suite est donc strictement décroissante.



Propriété
Soit (un) la suite définie explicitement par un = f (n), où f est une fonction définie sur R+, alors (un) a le même sens de variation que f:
  • si f est croissante, alors la suite (un) est croissante,
  • si f est décroissante, alors la suite (un) est décroissante.


Démonstration: Si par exemple f est croissante sur R+, alors f conserve l'ordre, c'est-à-dire que pour tous réels x≤y on a f (x)≤f (y).

On a ici un = f (n) et un+1 = f (n+1), et comme n≤n+1, on en déduit que f (n)≤ f (n+1) c'est-à-dire que un≤un+1, et donc que (un) est croissante.

Remarque: La réciproque est fausse.
Par exemple, soit la suite (un) définie par un = f(n) avec la fonction f(x) = x + sin(2πx).
Alors, pour tout entier n, un = n + sin(2πn) = n et donc (un) est croissante (c'est la suite des entiers naturels), tandis que f n'est pas monotone sur R.
Le graphique suivant montre cet échantillonnage croissant d'une fonction non monotone.
Suite croissante définie par une fonction non monotone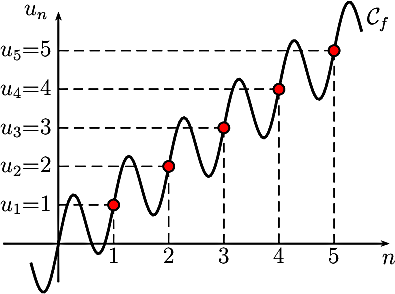
Contre exemple d'une suite croissante et fonction non croissante


Exercice 9
Étudier (de deux manières différentes !) le sens de variation des suites définies par:
  1. un = 3n−2/n+1
  2. un = −1/3n+3
  3. un = (n−5)2
  4. un = n−1+4/n+1
  5. un = n2−10n+26
  6. un = 2n3−30n2+54n





Voir aussi:
LongPage: h2: 3 - h3: 2