Devoir de maths corrigé, Fonction exponentielle
Première générale, spécialité mathématiques
Devoir de mathématiques, et corrigé, sur le produit scalaire et les probabilités conditionnelles et arbre de probabilités. Devoir posé en spé maths, première générale, année scolaire 2024/2025
Exercice 1: Calculs de fonctions dérivées avec exponentielles
Résoudre les équations et inéquations:
 ,
,
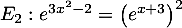 ,
,
 et
et
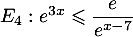
Cacher la correction
Correction exercice 1
-
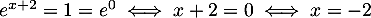 , donc
, donc 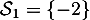
-
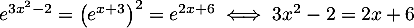 , car la fonction exponentielle est strictement croissante, et donc
, car la fonction exponentielle est strictement croissante, et donc
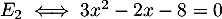 .
.
Cette équation du second degré a pour dsicriminant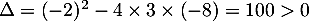 et admet donc deux solutions réelles
et admet donc deux solutions réelles
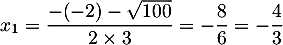 et
et 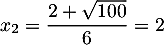 .
.
Ainsi,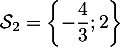
-
 car la fonction exponentielle est strictement croissante, et donc
car la fonction exponentielle est strictement croissante, et donc
 , soit les solutions
, soit les solutions
![$\mathcal{S}_3=]-\infty ; -3[$](/Generateur-Devoirs/1S/ChapExp/exeqinq_c/11.png)
- En multipliant par
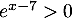 , donc l'ordre ne change pas, on obtient
, donc l'ordre ne change pas, on obtient
![\[E_4 \iff e^{3x}e^{x-7}=e^{4x-7}\leqslant e=e^1\]](/Generateur-Devoirs/1S/ChapExp/exeqinq_c/13.png)
et, comme la fonction exponentielle est strictement croissante,
![\[E_4\iff 4x-7\leqslant 1\iff x\leqslant2\]](/Generateur-Devoirs/1S/ChapExp/exeqinq_c/14.png)
soit donc les solutions![$\mathcal{S}_4=]-\infty ; 2]$](/Generateur-Devoirs/1S/ChapExp/exeqinq_c/15.png)
Cacher la correction
Exercice 2: Tableaux de signes
Étudier le sens de variation de la fonction 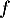 définie par
définie par
 .
.
Préciser l'équation de la tangente au point d'abscisse 0.
On a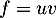 avec
avec  donc
donc 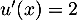 et
et 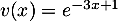 soit
soit 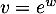 avec
avec
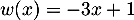 donc
donc 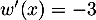 et alors
et alors 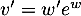 soit
soit 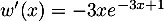 .
.
On a alors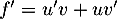 , soit
, soit
![\[f'(x)=2e^{-3x+1}+2x\times \lp-3e^{-3x+1}\rp=\lp -6x+2\rp e^{-3x+1}\]](/Generateur-Devoirs/1S/ChapExp/exvtpc_c/11.png)
L'exponentielle est toujours strictement positive,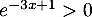 et on a dresse alors le tableau de signe et de variation:
et on a dresse alors le tableau de signe et de variation:
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $-\infty$ && $1/3$ && $+\infty$ \\\hline
$e^{-3x+1}$ && + &$|$& +&\\\hline
$-6x+2$ && $+$ &\zb&$-$ &\\\hline
$f'(x)$ && $+$ &\zb&$-$ &\\\hline
&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exvtpc_c/13.png)
L'équation de la tangente en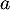 est
est
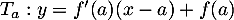 , soit ici avec
, soit ici avec  ,
,
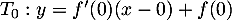 ,
donc ici, avec
,
donc ici, avec 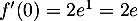 et
et 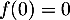 , on trouve l'équation
, on trouve l'équation
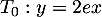
Cacher la correction
Préciser l'équation de la tangente au point d'abscisse 0.
Correction exercice 2
On a
On a alors
L'exponentielle est toujours strictement positive,
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $-\infty$ && $1/3$ && $+\infty$ \\\hline
$e^{-3x+1}$ && + &$|$& +&\\\hline
$-6x+2$ && $+$ &\zb&$-$ &\\\hline
$f'(x)$ && $+$ &\zb&$-$ &\\\hline
&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exvtpc_c/13.png)
L'équation de la tangente en
Cacher la correction
Exercice 3: Dérivée et équations de tangentes
Soit  la suite définie pour tout entier naturel
la suite définie pour tout entier naturel 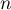 par
par
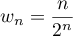 .
.
Déterminer le sens de variation de la suite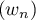 .
.
Pour tout entier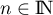 ,
,
![\[\begin{array}{ll}w_{n+1}-w_n&=\dfrac{n+1}{2^{n+1}}-\dfrac{n}{2^n}\\
&=\dfrac{1}{2^n}\left( \dfrac{n+1}{2}-n\rp\\
&=\dfrac{1}{2^n}\left( \dfrac{-n+1}{2}\rp\\
&=\dfrac{-n+1}{2^{n+1}}\enar\]](/Generateur-Devoirs/1S/Chap9/ex2.01_c/2.png)
Or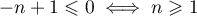 et ainsi
et ainsi
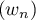 , ce qui signifie exactement que la suite
, ce qui signifie exactement que la suite
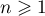 est décroissante.
est décroissante.
Cacher la correction
Déterminer le sens de variation de la suite
Correction exercice 3
Pour tout entier
![\[\begin{array}{ll}w_{n+1}-w_n&=\dfrac{n+1}{2^{n+1}}-\dfrac{n}{2^n}\\
&=\dfrac{1}{2^n}\left( \dfrac{n+1}{2}-n\rp\\
&=\dfrac{1}{2^n}\left( \dfrac{-n+1}{2}\rp\\
&=\dfrac{-n+1}{2^{n+1}}\enar\]](/Generateur-Devoirs/1S/Chap9/ex2.01_c/2.png)
Or
Cacher la correction
Exercice 4: Étude de fonction avec exponentielle et position relative
On définit la suite 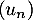 par
par 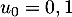 puis, pour tout entier naturel
puis, pour tout entier naturel 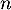 par la relation
par la relation
![\[u_{n+1}=-0,5u_n^2+1\]](/Generateur-Devoirs/1S/Chap9/exaraignee/4.png)
Le graphique suivant donne la courbe représentant la fonction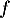 définie par l'expression
définie par l'expression 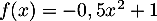 .
.
![\[\psset{unit=6cm,arrowsize=8pt}
\begin{pspicture*}(-.5,-.4)(2.3,1.5)
\psline{->}(-0.5,0)(2.3,0)
\psline{->}(0,-0.5)(0,1.5)
\multido{\i=0+1}{3}{%
\psline(\i,-0.02)(\i,0.02)%
\rput(\i,-0.08){$\i$}}
\multido{\i=0+1}{2}{
\psline(-0.05,\i)(0.05,\i)
\rput(-0.1,\i){$\i$}}
% Definition de la fonction f de u_{n+1}=f(u_n)
\newcommand{\f}[1]{-0.5 #1 2 exp mul 1 add}
% Et son tracer:
\psplot[linewidth=1.4pt]{0}{7}{\f{x}}
\rput(1.4,.2){$\mathcal{C}_f$}
\end{pspicture*}\]](/Generateur-Devoirs/1S/Chap9/exaraignee/13.png)
Cacher la correction
Le graphique suivant donne la courbe représentant la fonction
- Construire sur ce graphique, sur l'axe des abscisses, les premiers
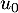 ,
, 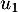 ,
, 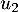 ,
, 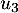 et
et 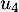 de la suite
de la suite 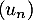 .
.
- Vers quelle valeur limite semble tendre cette suite ? Calculer la valeur exacte de cette limite.
![\[\psset{unit=6cm,arrowsize=8pt}
\begin{pspicture*}(-.5,-.4)(2.3,1.5)
\psline{->}(-0.5,0)(2.3,0)
\psline{->}(0,-0.5)(0,1.5)
\multido{\i=0+1}{3}{%
\psline(\i,-0.02)(\i,0.02)%
\rput(\i,-0.08){$\i$}}
\multido{\i=0+1}{2}{
\psline(-0.05,\i)(0.05,\i)
\rput(-0.1,\i){$\i$}}
% Definition de la fonction f de u_{n+1}=f(u_n)
\newcommand{\f}[1]{-0.5 #1 2 exp mul 1 add}
% Et son tracer:
\psplot[linewidth=1.4pt]{0}{7}{\f{x}}
\rput(1.4,.2){$\mathcal{C}_f$}
\end{pspicture*}\]](/Generateur-Devoirs/1S/Chap9/exaraignee/13.png)
Correction exercice 4
- On construit graphiquement les premiers termes de la suite en s'aidant de la droite d'équation
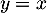
![\[\psset{unit=6cm,arrowsize=8pt}
\begin{pspicture*}(-.5,-.4)(2.3,1.5)
\psline{->}(-0.5,0)(2.3,0)
\psline{->}(0,-0.5)(0,1.5)
\multido{\i=0+1}{3}{%
\psline(\i,-0.02)(\i,0.02)%
\rput(\i,-0.08){$\i$}
}
\multido{\i=0+1}{2}{%
\psline(-0.02,\i)(0.02,\i)%
\rput(-0.1,\i){$\i$}%
}
% Definition de la fonction f de u_{n+1}=f(u_n)
\newcommand{\f}[1]{-0.5 #1 2 exp mul 1 add}
% Et son tracer:
\psplot[linewidth=1.4pt]{0}{7}{\f{x}}
\rput(1.4,.2){$\mathcal{C}_f$}
% ainsi que le tracer de la droite y=x
\psplot{-0.2}{6.5}{x}
\rput(1.4,1.2){$d:y=x$}
% Defintion de la fonction it\'er\'ee:
% par ex.: fn{3}{x}=f(f(f(x)))
\newcommand\fn[2]{%
\ifnum#1=1
\f{#2}%
\else
\f{\fn{\numexpr#1-1}{#2}}%
\fi
}
% Valeur initiale (u_0)
\def\xinit{0.1}
\def\nmax{4}
% Initialisation pour u_0
\psline[linestyle=dashed]
(\xinit,0)
(!\xinit\space\f{\xinit})
(!\f{\xinit}\space\f{\xinit})
\rput(\xinit,0){$\tm$}
\rput(\xinit,-0.07){$u_0$}
% Boucle pour u_1, u_2, ..., u_nmax
\multido{\i=1+1}{\nmax}{
\psline[linestyle=dashed]
(!\fn{\i}{\xinit} \space 0)
(!\fn{\i}{\xinit} \space \fn{\i}{\xinit})
(!\fn{\i}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
(!\fn{\numexpr\i+1}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
\rput(!\fn{\i}{\xinit}\space 0){$\tm$}
\rput(!\fn{\i}{\xinit}\space -0.07){$u_\i$}
}
\end{pspicture*}\]](/Generateur-Devoirs/1S/Chap9/exaraignee_c/2.png)
- La suite semble tendre vers la valeur
 qui est l'abscisse du point d'interection de la droite et de la courbe.
Cette valeur
qui est l'abscisse du point d'interection de la droite et de la courbe.
Cette valeur  est donc un point fixe pour la fonction
est donc un point fixe pour la fonction  , c'est-à-dire une valeur telle que
, c'est-à-dire une valeur telle que
![\[\begin{array}{ll}f(f)=l &\iff -0,5x^2+1=x\\[.4em] &\iff 0,5x^2+x-1=0\enar\]](/Generateur-Devoirs/1S/Chap9/exaraignee_c/6.png)
Cette équation du second degré a pour discriminant et admet donc deux racines
et admet donc deux racines
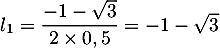 et
et 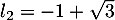 .
.
Comme la suite semble positive, la seule valeur limité possible est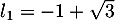 .
.
Cacher la correction
Exercice 5: Étude de fonction avec exponentielle et position relative
On définit la suite 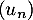 par
par
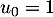 puis, pour tout entier
puis, pour tout entier 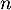 ,
,
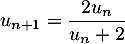 .
On suppose que cette suite est positive, c'est-à-dire que pour tout entier
.
On suppose que cette suite est positive, c'est-à-dire que pour tout entier 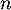 , on a
, on a 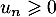 .
.
Cacher la correction
- Calculer les valeurs exactes des deux premiers termes de la suite,
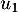 et
et 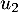 .
.
- Étudier le sens de variation de la suite
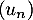 .
.
Correction exercice 5
-
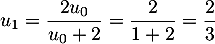 et
et
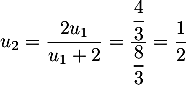
- On cherche le signe de la différence de deus termes consécutifs:
![\[\begin{array}{ll}u_{n+1}-u_n&=\dfrac{2u_n}{u_n+2}-u_n\\
&=\dfrac{2u_n}{u_n+2}-\dfrac{u_n(u_n+2)}{u_n+2}\\
&=\dfrac{-u_n^2}{u_n+2}\enar\]](/Generateur-Devoirs/1S/Chap9/ex1ervar_c/3.png)
Or et donc
et donc 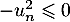 et, comme on suppose que
et, comme on suppose que 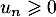 on a aussi le dénominateur
on a aussi le dénominateur  .
.
Finalement on a donc trouvé que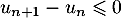 et donc que la suite
et donc que la suite 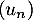 est décroissante.
est décroissante.
Cacher la correction
Quelques autres devoirs
Probabilités conditionnelles et calculs de probabilités avec un arbre de probabilités. Propriétés algébriques de l'exponentielle et une étude de fonctionDevoir: Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
étude de fonctions avec exponentielle, calculs de dérivées, et position relative d'une courbe et d'une droite
étude de fonctions avec exponentielle, premier devoir sur les suites: calcul des premiers termes et sens de variation, construction des premiers termes d'une suite
dérivée et sens de variation d'une fonction rationnelle - Calculs algébriques et équations avec exponentielles - Probabilités conditionnelles et arbre de probabilité
équations et inéquations avec exponentielles, variation de fonctions avec exponentielle, probabilités conditionnelle et arbre de probabilité
Quelques exercices corrigés
Exercices corrigés
Tangentes de l'exponentielle
Exercices corrigés
Expressions avec exponentielles à simplifiées
Exercices corrigés
Expressions avec exponentielles à simplifiées
Exercices corrigés
Deux équations avec exponentielles
Exercices corrigés
Deux équations et deux inéquations avec exponentielles
Voir aussi: