Suite récurrente, construction graphique des premiers termes
Exercice corrigé - Spécialité maths, première générale
Énoncé
Soit 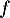 la fonction définie par
la fonction définie par 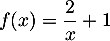 sur
sur ![$]0;+\infty[$](/Generateur-Devoirs/1S/Chap9/exrecgraph/3.png) .
.
On définit la suite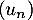 par
par 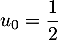 et, pour tout entier
et, pour tout entier 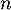 , par
, par 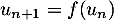 .
.
On définit la suite
- Calculer
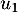 .
.
- Déterminer le sens de variation de
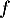 puis tracer l'allure de la courbe représentative de
puis tracer l'allure de la courbe représentative de 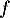 dans un repère.
dans un repère.
- Construire sur ce graphique les points
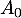 ,
, 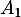 ,
, 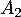 ,
, 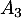 et
et 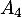 d'ordonnées nulles et d'absisses
d'ordonnées nulles et d'absisses 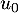 ,
, 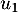 ,…,
,…,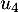 .
.
- Quelle conjecture peut-on faire quant-à la valeur limite de cette suite ? Calculer la valeur exacte de cette limite éventuelle.
Correction
Correction
-
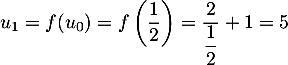 .
.
- On a
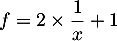 d'où
d'où 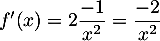 .
.
On trouve ainsi que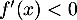 pour tout
pour tout ![$x\in]0;+\infty[$](/Generateur-Devoirs/1S/Chap9/exrecgraph_c/5.png) et donc que
et donc que 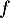 est strictement décroissante sur cete intervalle.
est strictement décroissante sur cete intervalle.
- On trace alors l'allure de la courbe et sur le graphique la droite d'équation
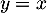 et on construit les points demandés sur l'axe des abscisses.
et on construit les points demandés sur l'axe des abscisses.
{\i}\psline(-.08,\i)(.05,\i)}
%\psplot{.1}{5}{2 x div 1 add}
% Definition de la fonction f de u_{n+1}=f(u_n)
\newcommand{\f}[1]{2 #1 div 1 add}
% Et son tracer:
\psplot[linewidth=1.4pt]{0.1}{7}{\f{x}}
% ainsi que le tracer de la droite y=x
\psplot{-.5}{6.5}{x}
% Defintion de la fonction it\'er\'ee:
% par ex.: fn{3}{x}=f(f(f(x)))
\newcommand\fn[2]{%
\ifnum#1=1
\f{#2}%
\else
\f{\fn{\numexpr#1-1}{#2}}%
\fi
}
% Valeur initiale (u_0)
\def\xinit{.5}
\def\nmax{4}
% Initialisation pour u_0
\psline[linestyle=dashed]
(\xinit,0)
(!\xinit\space\f{\xinit})
(!\f{\xinit}\space\f{\xinit})
\rput(\xinit,-0.3){$A_0$}
% Boucle pour u_1, u_2, ..., u_nmax
\multido{\i=1+1}{\nmax}{
\psline[linestyle=dashed]
(!\fn{\i}{\xinit} \space 0)
(!\fn{\i}{\xinit} \space \fn{\i}{\xinit})
(!\fn{\i}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
(!\fn{\numexpr\i+1}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
\rput(!\fn{\i}{\xinit}\space 0){$\tm$}
\rput(!\fn{\i}{\xinit}\space -0.3){$A_\i$}
}
\end{pspicture*}\]](/Generateur-Devoirs/1S/Chap9/exrecgraph_c/8.png)
- La suite semble tendre vers l'abscisse du point d'intersection entre la courbe de
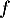 et la droite d'équation
et la droite d'équation 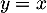 .
.
L'abscisse de ce point vérifie dont l'équation
![\[f(x)=x\iff\dfrac2x+1=x\]](/Generateur-Devoirs/1S/Chap9/exrecgraph_c/11.png)
soit, en multipliant par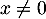 (car
(car 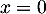 n'est pas solution),
n'est pas solution),
![\[2+x=x^2\iff x^2-x-2=0\]](/Generateur-Devoirs/1S/Chap9/exrecgraph_c/14.png)
Cette équation du second degré a pour discriminant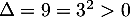 et admet donc deux solutions
et admet donc deux solutions 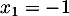 et
et 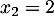 .
.
La première solution n'est pas celle recherchée, et la seule limite éventuelle est donc
n'est pas celle recherchée, et la seule limite éventuelle est donc 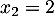 .
.
Tag:Suites
Voir aussi:
Quelques devoirs
étude de fonctions avec exponentielle, premier devoir sur les suites: calcul des premiers termes et sens de variation, construction des premiers termes d'une suite
variation d'une fonction composée avec une exponentielle - Deux inéquations avec des exponentielles - Suite numériques explicite et récurrente, construction graphique des premiers termes
Suites: construction graphique des premiers termes, suite intermédiaire arithmétique - Etude d'une suite récurrente avec une suite auxiliaire arithmétique
sur les suites: sommes des termes d'une suite arithmétique et géométrique. Etude d'une suite récurrente avec une suite auxiliaire. Suite récurrente définie avec une fonction exponentielle. Balle rebondissante: hauteur des rebonds et distance totales parcourue
fin d'année, sur les fonctions, exponentielle, suite et variable aléatoire
