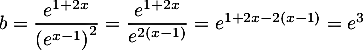Devoir de maths corrigé, Dérivées et produit scalaire
Première générale, spécialité mathématiques
Devoir de mathématiques, et corrigé, posé en spé maths, première générale, année scolaire 2023/2024
Exercice 1: Variation d'une fonction rationnelle et équation d'une tangente
Dresser le tableau de variation de la fonction 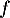 définie par
définie par
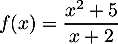 .
.
Donner l'équation de la tangente à la courbe de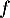 au point d'abscisse 1.
au point d'abscisse 1.
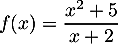 .
On a
.
On a 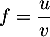 ,
avec
,
avec 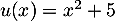 donc
donc 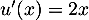 ,
et
,
et 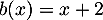 donc
donc 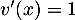 .
.
On a donc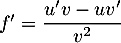 ,
soit
,
soit
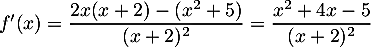
Le numérateur et un trinôme du second degré qui a pour discriminant a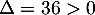 et admet donc deux racines:
et admet donc deux racines:
 et
et 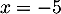 .
.
Le dénominateur s'annule en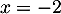 qui est donc une valeur interdite.
qui est donc une valeur interdite.
![\[\begin{tabular}{|c|ccccccccc|}\hline
$x$ & $-\infty$ && $-5$ && $-2$ && 1 && $+\infty$ \\\hline
$x^2+4x-5$ && $+$ &\zb& $-$ &$|$ & $-$ &\zb & $+$ & \\\hline
$(x+2)^2$ && $+$ &$|$& $+$ &\zb& $+$ &$|$ & $+$ & \\\hline
$f'(x)$ && $+$ &\zb& $-$ & & $-$ &\zb & $+$ & \\\hline
&&&&&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\psline(0,-.6)(0,1.3)\,\psline(0,-.6)(0,1.3)&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exvar2_c/13.png)
La tangente au point d'abscisse 1 a pour équation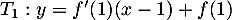 ,
avec
,
avec 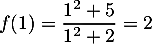 et
et 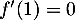 , d'où l'équation
, d'où l'équation
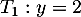 : la tangente est horizontale.
: la tangente est horizontale.
Cacher la correction
Donner l'équation de la tangente à la courbe de
Correction exercice 1
On a donc
Le numérateur et un trinôme du second degré qui a pour discriminant a
Le dénominateur s'annule en
![\[\begin{tabular}{|c|ccccccccc|}\hline
$x$ & $-\infty$ && $-5$ && $-2$ && 1 && $+\infty$ \\\hline
$x^2+4x-5$ && $+$ &\zb& $-$ &$|$ & $-$ &\zb & $+$ & \\\hline
$(x+2)^2$ && $+$ &$|$& $+$ &\zb& $+$ &$|$ & $+$ & \\\hline
$f'(x)$ && $+$ &\zb& $-$ & & $-$ &\zb & $+$ & \\\hline
&&&&&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\psline(0,-.6)(0,1.3)\,\psline(0,-.6)(0,1.3)&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exvar2_c/13.png)
La tangente au point d'abscisse 1 a pour équation
Cacher la correction
Exercice 2: Expressions avec exponentielles à simplifiées
Exercice 3: Deux équations avec exponentielles
Résoudre les équations 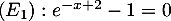 et
et 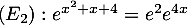
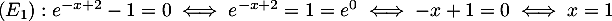
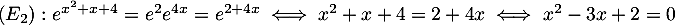
Cette équation du second degré a pour discriminant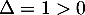 et admet donc deux racines
et admet donc deux racines  et
et 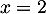 qui sont donc les solutions de
qui sont donc les solutions de 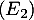 .
.
Cacher la correction
Correction exercice 3
Cette équation du second degré a pour discriminant
Cacher la correction
Exercice 4: Probabilités conditionnelles: lien entre malformation cardiaque et anévrisme
En utilisant sa base de données, la sécurité sociale estime que la proportion de Français présentant, à la naissance, une malformation cardiaque de type anévrisme est de 10%. L'étude a également permis de prouver que 30% des Français présentant, à la naissance, une malformation cardiaque de type anévrisme, seront victimes d'un accident cardiaque au cours de leur vie alors que cette proportion n'atteint plus que 8% pour ceux qui ne souffrent pas de cette malformation congénitale.
On choisit au hasard une personne dans la population française et on considère les évènements :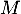 : « La personne présente, à la naissance, une malformation cardiaque de type anévrisme »
: « La personne présente, à la naissance, une malformation cardiaque de type anévrisme »
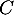 : « La personne est victime d'un accident cardiaque au cours de sa vie ».
: « La personne est victime d'un accident cardiaque au cours de sa vie ».
On peut construire l'arbre pondéré suivant:
![\[\psset{xunit=1.5cm,yunit=1cm}
\begin{pspicture}(-2,-2.)(5,2)
\psline(0,0)(1.5,1.5)\rput(1.75,1.5){$M$}\rput(0.7,1.2){$0,10$}
\psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$C$}\rput(2.7,2.2){$0,30$}
\psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{C}$}\rput(2.7,0.7){$0,70$}
%
\psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$\overline{M}$}\rput(0.7,-1.2){$0,90$}
\psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$C$}\rput(2.7,-0.7){$0,08$}
\psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{C}$}\rput(2.7,-2.2){$0,92$}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap7/exsecu_c/1.png)
Cacher la correction
On choisit au hasard une personne dans la population française et on considère les évènements :
-
- Quelle est la probabilité que la personne présente une malformation cardiaque de type anévrisme et soit victime d'un accident cardiaque au cours de sa vie.
- Calculer
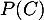 .
.
- On choisit au hasard une victime d'un accident cardiaque. Quelle est la probabilité qu'elle présente une malformation cardiaque de type anévrisme ?
Correction exercice 4
On peut construire l'arbre pondéré suivant:
![\[\psset{xunit=1.5cm,yunit=1cm}
\begin{pspicture}(-2,-2.)(5,2)
\psline(0,0)(1.5,1.5)\rput(1.75,1.5){$M$}\rput(0.7,1.2){$0,10$}
\psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$C$}\rput(2.7,2.2){$0,30$}
\psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{C}$}\rput(2.7,0.7){$0,70$}
%
\psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$\overline{M}$}\rput(0.7,-1.2){$0,90$}
\psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$C$}\rput(2.7,-0.7){$0,08$}
\psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{C}$}\rput(2.7,-2.2){$0,92$}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap7/exsecu_c/1.png)
-
-
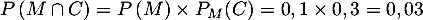
- En utilisant l'arbre (ou d'après la formule des probabilités totales):
![\[\begin{array}{ll}
P(C)&=P\left( M \cap C\right) + P\left(\overline M \cap C\right)\\[0.3cm]
&= P(M)\times P_M(C) + P\lp\overline M\rp\times P_{\overline M}(C) \\[0.3cm]
&= 0,1\times 0,3 + 0,9 \times 0,08 = 0,03 + 0,072 = 0,102\enar\]](/Generateur-Devoirs/1S/Chap7/exsecu_c/3.png)
-
- On choisit au hasard une victime d'un accident cardiaque.
La probabilité qu'elle présente une malformation cardiaque de type anévrisme est
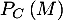 :
:
Cacher la correction
Quelques autres devoirs
second degré (équation et inéquation, tableau de signe). Dérivabilité d'une fonction en un point: taux d'accroissement et nombre dérivé (calcul et lecture graphique)
fonctions dérivées, étude de fonction et position relative de deux courbes
dérivées et étude de fonction. Angles en radians sur le cercle trigonométrique et en mesure principale
Géométrie avec le produit scalaire, projeté orthogonal et calcul d'un angle et droites tangentes à une parabole perpendiculaires
Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
Quelques exercices corrigés
Exercices corrigés
Cours: définition graphique du nombre dérivé
Exercices corrigés
Calcul du nombre dérivé et tangente
Exercices corrigés
Calculs de dérivées
Exercices corrigés
Calculs de fonctions dérivées
Exercices corrigés
Fonctions dérivées
Voir aussi:
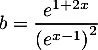 ,
,