Calcul des premieres termes et variation d'une suite récurrente
Exercice corrigé - Spécialité maths, première générale
Énoncé
On définit la suite 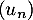 par
par
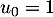 puis, pour tout entier
puis, pour tout entier 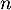 ,
,
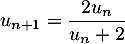 .
On suppose que cette suite est positive, c'est-à-dire que pour tout entier
.
On suppose que cette suite est positive, c'est-à-dire que pour tout entier 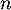 , on a
, on a 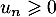 .
.
- Calculer les valeurs exactes des deux premiers termes de la suite,
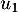 et
et 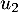 .
.
- Étudier le sens de variation de la suite
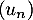 .
.
Correction
Correction
-
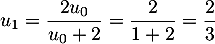 et
et
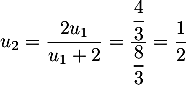
- On cherche le signe de la différence de deus termes consécutifs:
![\[\begin{array}{ll}u_{n+1}-u_n&=\dfrac{2u_n}{u_n+2}-u_n\\
&=\dfrac{2u_n}{u_n+2}-\dfrac{u_n(u_n+2)}{u_n+2}\\
&=\dfrac{-u_n^2}{u_n+2}\enar\]](/Generateur-Devoirs/1S/Chap9/ex1ervar_c/3.png)
Or et donc
et donc 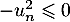 et, comme on suppose que
et, comme on suppose que 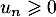 on a aussi le dénominateur
on a aussi le dénominateur  .
.
Finalement on a donc trouvé que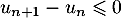 et donc que la suite
et donc que la suite 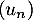 est décroissante.
est décroissante.
Tag:Suites
Voir aussi:
Quelques devoirs
étude de fonctions avec exponentielle, premier devoir sur les suites: calcul des premiers termes et sens de variation, construction des premiers termes d'une suite
variation d'une fonction composée avec une exponentielle - Deux inéquations avec des exponentielles - Suite numériques explicite et récurrente, construction graphique des premiers termes
Suites: construction graphique des premiers termes, suite intermédiaire arithmétique - Etude d'une suite récurrente avec une suite auxiliaire arithmétique
sur les suites: sommes des termes d'une suite arithmétique et géométrique. Etude d'une suite récurrente avec une suite auxiliaire. Suite récurrente définie avec une fonction exponentielle. Balle rebondissante: hauteur des rebonds et distance totales parcourue
fin d'année, sur les fonctions, exponentielle, suite et variable aléatoire
