Devoir de maths corrigé, Exponentielle et probabilités conditionnelles
Première générale, spécialité mathématiques
Devoir de mathématiques, et corrigé, posé en spé maths, première générale, année scolaire 2023/2024
Exercice 1: Deux équations et deux inéquations avec exponentielles
Exercice 2: sens de variation de fonctions composées avec exponentielles et équations de tangentes
On considère la fonction 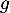 définie par
définie par 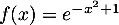 .
.
Déterminer les équations des tangentes à la courbe de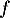 aux points d'abscisses
aux points d'abscisses 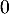 et
et 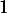 .
.
On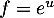 avec
avec 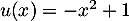 donc
donc 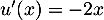 ,
et alors
,
et alors 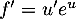 , soit
, soit 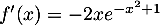 .
.
L'équation de la tangente en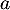 est
est 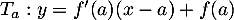 et donc les deux équations,
et donc les deux équations,
en 0: avec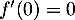 et
et 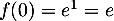 , on obtient
, on obtient
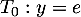
en 1: avec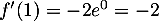 et
et 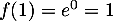 , on obtient
, on obtient
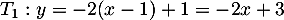
Cacher la correction
Déterminer les équations des tangentes à la courbe de
Correction exercice 2
On
L'équation de la tangente en
en 0: avec
en 1: avec
Cacher la correction
Exercice 3: Variation d'une fonction produit avec exponentielle
Étudier le sens de variation de la fonction 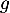 définie par
définie par
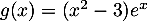
On a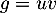 avec
avec 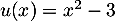 donc
donc 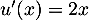 et
et 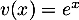 donc
donc 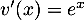 .
.
Ainsi,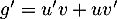 , soit
, soit
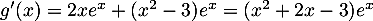
On a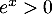 et le premier terme est du second degré de discriminant
et le premier terme est du second degré de discriminant 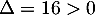 et admet donc deux racines
et admet donc deux racines 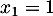 et
et 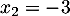 .
.
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-3$ && 1 &&$+\infty$ \\\hline
$x^2+2x-3$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ &\mbox{$0\hspace{-0.67em}\mid$}& $+$ &\\\hline
$e^x$ && $+$&$|$& $+$ & $|$ & $+$&\\\hline
$g'(x)$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ &\mbox{$0\hspace{-0.67em}\mid$}& $+$ &\\\hline
&&&&&&&\\
$g$&&\Large{$\nearrow$}&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exvarproduit_c/12.png)
Cacher la correction
Correction exercice 3
On a
Ainsi,
On a
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-3$ && 1 &&$+\infty$ \\\hline
$x^2+2x-3$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ &\mbox{$0\hspace{-0.67em}\mid$}& $+$ &\\\hline
$e^x$ && $+$&$|$& $+$ & $|$ & $+$&\\\hline
$g'(x)$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ &\mbox{$0\hspace{-0.67em}\mid$}& $+$ &\\\hline
&&&&&&&\\
$g$&&\Large{$\nearrow$}&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exvarproduit_c/12.png)
Cacher la correction
Exercice 4: Probabilités conditionnelles: Vélo ou bus pour se rendre au lycée
Un élève doit se rendre à son lycée chaque matin pour 8h00. Pour cela, il utilise, selon les jours, deux moyens de transport : le vélo ou le bus.
L'élève part tous les jours à 7h40 de son domicile et doit arriver à 8h00 à son lycée. Il prend le vélo 7 jours sur 10 et le bus le reste du temps.
Les jours où il prend le vélo, il arrive à l’heure dans 99,4% des cas et lorsqu’il prend le bus, il arrive en retard dans 5% des cas.
On choisit une date au hasard en période scolaire et on note les événements
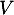 : « L'élève se rend au lycée à vélo»
: « L'élève se rend au lycée à vélo»
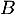 : « l'élève se rend au lycée en bus»
: « l'élève se rend au lycée en bus»
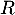 : « L’élève arrive en retard au lycée».
: « L’élève arrive en retard au lycée».
Cacher la correction
L'élève part tous les jours à 7h40 de son domicile et doit arriver à 8h00 à son lycée. Il prend le vélo 7 jours sur 10 et le bus le reste du temps.
Les jours où il prend le vélo, il arrive à l’heure dans 99,4% des cas et lorsqu’il prend le bus, il arrive en retard dans 5% des cas.
On choisit une date au hasard en période scolaire et on note les événements
- Traduire la situation par un arbre de probabilités.
- Déterminer la probabilité de l’événement
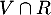 .
.
- Démontrer que la probabilité de l’événement R est 0,0192
- Un jour donné, l'élève est arrivé en retard au lycée. Quelle est la probabilité qu'il s'y soit rendu en bus ?
Correction exercice 4
-
![\[\psset{xunit=1cm,yunit=.6cm}
\begin{pspicture}(-2,-3)(5,2.)
\psline(0,0)(1.5,1.5)\rput(1.75,1.5){$V$}\rput(.7,1.3){$7/10$}
\psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$R$}\rput(2.7,2.3){$0,6\%$}
\psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{R}$}\rput(2.7,.6){$99,4\%$}
\psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$B$}\rput(.7,-1.3){$3/10$}
\psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$R$}\rput(2.7,-.6){$5\%$}
\psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{R}$}\rput(2.7,-2.4){$95\%$}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap7/exvelobus_c/1.png)
-
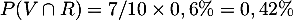
- D'après la formule des probabilités totales,
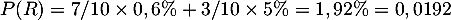
- On cherche la probabilité conditionnelle
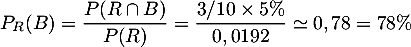
Cacher la correction
Exercice 5: Etude d'une fonction rationnelle avec exponentielles
On considère la fonction 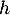 définie par l'expression
définie par l'expression 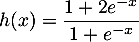
Montrer que, pour tout réel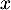 , on a
, on a 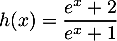 .
.
Étudier alors les variations de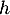 .
.
On a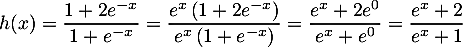 .
.
On a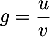 avec
avec 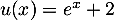 , donc
, donc 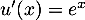 et
et 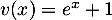 , donc
, donc 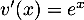 .
.
On obtient alors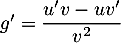 soit
soit 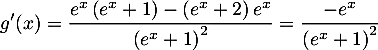
De plus, pour tout réel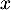 , on a
, on a 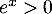 et donc
et donc 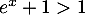 et en particulier
et en particulier 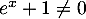 et donc
et donc 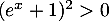 .
.
![\[\begin{tabular}{|c|ccc|}\hline $x$ & $-\infty$ && $+\infty$ \\\hline $-e^x$ && $-$ &\\\hline $\left( e^x+1\rp^2$ && $+$ &\\\hline $g'(x)$ && $-$ &\\\hline &2&&\\ $g$&&\Large{$\searrow$}&\\ &&&1\\\hline \end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exexpratio_c/14.png)
Cacher la correction
Montrer que, pour tout réel
Étudier alors les variations de
Correction exercice 5
On a
On a
On obtient alors
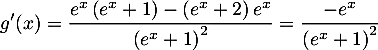
De plus, pour tout réel
![\[\begin{tabular}{|c|ccc|}\hline $x$ & $-\infty$ && $+\infty$ \\\hline $-e^x$ && $-$ &\\\hline $\left( e^x+1\rp^2$ && $+$ &\\\hline $g'(x)$ && $-$ &\\\hline &2&&\\ $g$&&\Large{$\searrow$}&\\ &&&1\\\hline \end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exexpratio_c/14.png)
Cacher la correction
Quelques autres devoirs
Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
Probabilités conditionnelles et calculs de probabilités avec un arbre de probabilités. Propriétés algébriques de l'exponentielle et une étude de fonctionDevoir: Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
étude de fonctions avec exponentielle, calculs de dérivées, et position relative d'une courbe et d'une droite
une étude des variations d'une fonction - Calcul de la valeur approchée d'un angle avec le produit scalaire dans un repère - Probabilités conditionnelles et réunion / intersection d'événements
une étude des variations d'une fonction - Calcul de la valeur approchée d'un angle avec le produit scalaire dans un repère - Probabilités conditionnelles et réunion / intersection d'événements
Quelques exercices corrigés
Exercices corrigés
Réunion, intersection et incompatibilité
Exercices corrigés
Réunion, intersection et contraire
Exercices corrigés
Réunion et intersection, cartes à puces avec deux défauts
Exercices corrigés
Gâteaux à la crème et aux fruits
Exercices corrigés
Efficacité de stages de révision dans une université
Voir aussi: