≡ Maths appliquées et applications des maths

Principe de fonctionnement du GPS


Introduction

Le Global Positioning System (GPS), que l'on peut traduire en français par "système de positionnement, ou de localisation, mondial", est un système de (géo)localisation fonctionnant au niveau mondial.
Le GPS est à l'origine, dans les années 60, un projet de recherche de l'armée américaine qui voit le jour en pratique dès 1978 avec les premiers lancements de satellites dédiés à cette tâche.
Le système fut alors très rapidement autorisé pour un usage civil (décision en 1983 de Ronald Reagan, suite à la mort des nombreux passagers d'un vol civil).
De nombreuses sciences sont initialement très désireuses de ce genre de ce système, comme bien évidemment les sciences géographiques et la cartographie.

Le succès rencontré par ce système a ensuite bouleversé de nombreux secteurs comme la navigation, maritime et aérienne, la géodésie [1], la cartographie et les travaux topographiques les plus courants, ainsi que tous les domaines scientifiques et technologiques nécessitant la connaissance précise de certaines positions (mécanique, tectonique des plaques, aéronautique, ...).

Le GPS permet le calcul de la positon d'un système, équipé du récepteur et calculateur adéquat, à partir de satellites de communication mis en orbite à cette fin.

Satellite de communication

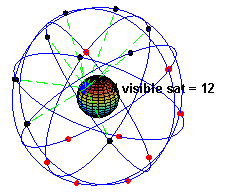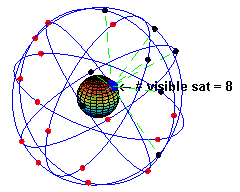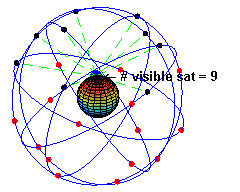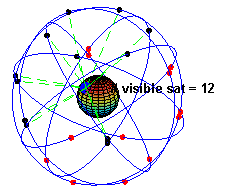
Le premier satellite de communication fut lancé en 1978. D'autres lancements suivirent pour atteindre une constellation de 24 satellite en 1995, puis actuelllement (depuis 2010) de 31 satellites. Cette constellation a été conçue de telle manière que, en tout point de la Terre et à tout moment, quatre satellites au moins soient visibles (voir figure 2).
La figure 1 illustre un de ces satellites de communication.


Illustration du satellite de communication Milstar
Fig. 1: Satellite de communication militaire Milstar des États-Unis.


Ces satellites de communication sont des satellites artificiels placés dans l'espace, en orbite terrestre à une altitude d'environ 20 000 km (entre 20 000 et 20 500 km). Ils suivent une orbite quasi-circulaire qu'ils parcourent en un peu moins de 12 h (11h 58min et 2s, soit un demi-jour sidéral).
Vus du sol, ces satellites reviennent donc chaque jour sidéral à la même position dans le ciel.


Animation de la constellation des satellites GPS gravitant autour de la Terre
Fig. 2: La constellation des satellites du GPS

Les positions de ces satellites sont connues à tout moment, en particulier par un récepteur GPS, et vont alors justement être utilisées pour déterminer la position de ce récepteur.

Ces satellites émettent des ondes électromagnétiques dans tout l'espace (et en particulier en direction de la Terre, et donc d'un éventuel récepteur terrestre).
La vitesse de propagation de ces ondes étant connue (environ 300 000 km par seconde), on peut en mesurant le temps que l'onde a mis pour parcourir le trajet satellite / récepteur, en déduire la distance entre le récepteur et le satellite (dont la position est supposée connue).


Des détails spécifiques à la communication de signaux numériques entre un émetteur et un récepteur distincts physiquement peuvent-être trouvés à la rubrique Communication numérique: Transmission d'informations entre systèmes numériques.

Mesure de la distance à un émetteur

Une onde électromagnétique est caractérisée par sa fréquence $f$. Les satellites de communications utilisés par le GPS communiquent sur deux fréquences: 1 575,42 MHz et 1 227,60 MHz [2].

Dans le vide, ou l'air qui y est assimilable, une telle onde se propage à la vitesse $ c=300\,000$ km par seconde (soit environ $ c=1$ milliard de kilomètres par heure !).


Animation représentant l'émission et la propagation d'une onde
Fig.3:Emission d'une onde par une source (rouge)
dans l'espace contenant un récepteur (noir).



Animation représentant l'émission et la propagation d'une onde par un satellite vers la Terre
Fig.4:Emission d'une onde par un satellite
dont une partie éclaire la Terre.
Dans ces conditions, si l'onde parcourt la distance séparant l'émetteur au récepteur en $t$ secondes, on peut en déduire directement que cette distance entre les deux élèments est donnée par $d=c\times t$. Ainsi, à partir de la mesure de la durée de la propagation du signal, on peut en déduire la distance entre le récepteur et la source.

A ce stade, connaissant la distance $d$ entre notre récepteur et l'émetteur, on en déduit que l'on se trouve sur un cercle de rayon $d$ centré sur l'émetteur. De la même façon, dans l'espace, on détermine la distance entre le récepteur et le satellite. On en déduit cette fois que nous nous trouvons (avec notre notre récepteur) sur une sphère de rayon $d$ centrée sur le satellite.

Cette information est donc insuffisante pour situer explicitement le récepteur.
En réitérant cette opération avec d'autres satellites dont le signal est accessible par le récepteur au moment donné, on peut alors en déduire qu'on se trouve sur plusieurs sphères simultanément, c'est-à-dire à l'intersection de ces sphères.

Intersection de sphères


L'intersection de deux sphères, comme illustré sur la figure 5 ci-contre, est un cercle.
Ainsi, ayant capté les signaux de deux satellites, on sait alors qu'on se trouve quelque part sur ce cercle.
L'information donnée par deux satellites est donc encore trop faible pour localiser sans ambiguité un point.
Intersection de 2 sphères = un cercle
Fig.5:Intersection de deux sphères: un cercle


Imaginons maintenant que l'on capte, toujours au même moment, le signal émis par un troisième satellite.
Cela revient à ajouter une troisième sphère (centrée sur ce troisième satellite) à notre graphique précédent.
L'intersection de ces trois sphères, comme illustré sur la figure 6 ci-contre, se réduit alors à deux points.

On peut alors, en général, retirer un de ces deux points comme fournissant une localisation aberrante (on est sur la Terre quand même...).
Le point restant est la localisation recherchée.
Intersection de 3 sphères = 2 points
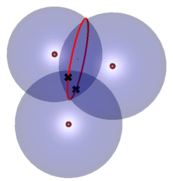
Fig.6: Intersection de trois sphères:
le cercle intersection de deux des sphères
intersecte la 3ème sphère en deux points.

Géolocalisation

Le principe précédent est utilisé pour localiser un point sur la Terre (géo-localisation).

En général, quatre satellites sont en fait utilisés pour localiser un point. L'information est alors redondante, et permet de gagner en précision (de l'ordre de 25 m initialement) (voir aussi ci-dessous les sources d'erreur).
La plupart des satellites sont en fait même capables d'affiner leurs calculs en utilisant plus de quatre satellites, tout en discriminant les satellites peu fiables (dont le signal reçu semble trop perturbé) ou encore trop proches les uns des autres (manque de pertinence dans l'information).
Géolocalisation comme intersection de 3 sphères autour de 3 satellites Fig.7:Géolocalisation à l'aide de trois satellites
Au contraire des exemples simples précédents utilisants deux ou trois sphères fixes, il faut se rappeler qu'il s'agit ici de satellites de communication en orbite, et en particulier en mouvement.
Le récepteur doit donc être en mesure de déterminer à tout instant la position de chacun des 31 satellites et de quel satellite provient le signal reçu.

Les satellites émettent donc en continu un signal permettant de déterminer l'heure de son envoi ainsi que son identification.

Les satellites GPS sont, grosso-modo, des horloges parlantes qui fournissent l'heure en permanence à tout récepteur GPS dans son champ.

Sources d'erreur

  • Qualité de la mesure temporelle. On a vu que la distance séparant le récepteur GPS aux satellites était mesurée indirectement, par le biais de la mesure du temps de propagation entre les deux éléments d'une onde électromagnétique.
    Cette vitesse de propagation ($c=300\,000$ km/s) étant très importante, la qualité de la mesure doit être en conséquence. En effet, une erreur par exemple de 1 seconde sur la mesure implique une erreur sur la distance mesurée de 300 000 km ! c'est-à-dire une mesure complètement aberrante.
    Pour obtenir une précision en distance de l'ordre du mètre, il faut donc que les durées soient mesurables avec une précision de l'ordre du dixième ou centième de microsecondes (soit un dixième de millionnième de seconde).
    Pour répondre à cette attente, le signal émis par chaque satellite est calé sur une horloge atomique [3], tandis qu'un récepteur est équipé quant à lui de plusieurs horloges atomiques.

  • Effet de l'atmosphère. Le signal émis par les satellites est un signal relativement faible. Celui-ci peut-être perturbé de manière non négligeable lors de la traversée des couches de l'atmosphère.
    Par exemple, la troposphère, couche basse de l'atmosphère, peut présenter des modifications du taux d'humidité et de pressions importantes. Ceci influe donc directement sur l'indice de l'air, donc sur la vitesse et la direction de propagation des ondes électromagnétiques. La correction directe de ce type d'erreur est délicate, car elle nécessiterait la connaissance de paramètres difficilement collectables.
    De la même façon, l'ionosphère, couche supérieure de l'atmosphère ionisée par le rayonnement solaire, peut aussi modifier la vitesse de propagation des ondes électromagnétiques. La correction est là aussi assez complexe directement, car nécessitant la prise en compte de l'évolution de l'activité solaire.
    Néanmoins, certains récepteurs peuvent capter les signaux émis par les satellites aux deux fréquences d'émission (récepteurs bi-fréquences, ou bi-bandes à l'instar des téléphones portables possédant cette caractéristique). Les modifications de la vitesse et de la direction du signal est dépendante de sa fréquence. Ainsi les signaux aux deux fréquences ne sont pas affectés de la même façon, et il est alors possible de calculer la perturbation réelle et donc de la corriger.

  • Effet du relief et de l'environnement. De la même façon que précédemment, le relief et l'environnement peuvent introduire des perturbations sur le signal reçu. L'environnement peut, par exemple, tout simplement cacher le satellite (sommet montagneux, bâtiment urbain, ...) au récepteur. Les satellites étant en mouvement (et souvent l'usager aussi), cette situation peut n'être que ponctuelle.
    Plus ennuyeux encore sont les perturbations dues à des réflexions des signaux sur le relief. En effet, le trajet du signal est alors artificiellement augmenté, et les mesures et calculs effectués par le récepteur peuvent se révéler complètement aberrants.
    Dans tous les cas, la prise en compte des signaux d'un nombre important de satellites permet d'affiner, de rectifier, voire de corriger certaines erreurs si elles n'affectent qu'un faible nombre de signaux (idéalement, il doit rester au moins trois ou quatre satellites non perturbés).



Améliorations de la précision

Il existe différentes méthodes permettant d'augmenter la précision des mesures calculées par un simple récepteur GPS.
  • Couplage avec le réseau IGN. Il est possible par exemple de coupler les données et calculs réalisés par un récepteur GPS avec le réseau de bornes IGN mis en place par l'IGN (Institut Géographique National). Avec ce réseau est associé un système de coordonnées particulier qui permet de mieux exploiter les données calculées par un récepteur GPS.

  • mode de positionnement différentiel. Cette méthode de correction est basée sur l'utilisation d'une combinaison de deux récepteurs qui observent les mêmes satellites au même instant, et qui communiquent entre eux.
    Le premier récepteur est placé en un point dont les coordonnées sont connues, tandis que le deuxième se trouve en un lieu à déterminer (précisément...). Le premier récepteur peut alors comparer les données qu'il reçoit et calcule sur sa position par rapport à celle connues (entrées par un utilisateur). Il peut alors en déduire les corrections à apporter pour calibrer précisément ses mesures, et les transmettre au deuxième récepteur qui pourra corriger convenablement ses propres mesures (les données étant reçues des mêmes satellites, les erreurs sont supposées être identiques).


[1] Science, initialement destinée au tracé des cartes, qui a pour objectif la détermination de la forme et des dimensions de la Terre: c'est la science qui "mesure et représente la surface terrestre".
Il s'agit aussi, par extension, de la discipline mathématique qui traite des méthodes et opérations nécessaires pour représenter une carte, effectuer des mesures sur une carte (mesurer un arc, un méridien, une distance entre deux points, ...). Retour

[2] Pour information, la norme GSM (Global System for Mobile Communications, ou "système mondial pour les communications mobiles") utilise les gammes des fréquences aux alentour de 900 MHz et de 1 900 MHz. Retour

[3] Une horloge atomique fonctionne sur le principe de l'asservissement d'un oscillateur à quartz sur le rayonnement émis lors d'une transition atomique entre deux niveaux d'une structure hyperfine.
Lors du passage d'un électron entre deux niveaux d'énergie, un rayonnement électromagnétique est émis à une fréquence très particulière qui permet d'exciter l'oscillateur à quartz.
Avec de telles horloges, l'inexactitude des étalons de fréquence s'est vue réduite en valeur relative à environ $10^{-12}$.

La définition actuelle de la seconde repose aussi sur un tel principe. La seconde est : la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins de l'état fondamental de l'atome de césium. Retour

* Les graphiques et animations de cette page ont été réalisés sous Matlab:

Voir aussi:




LongPage: h2: 7 - h3: 0