Numérisation d'un signal

Introduction
Codage binaire d'un nombre
Numérisation d'un signal
Reconstruction du signal original après numérisation

Introduction

Vers la fin des années 30, Claude Shannon démontra qu'à l'aide de "contacteurs", c'est-à-dire d'interrupteurs, il était possible d'effectuer des opérations logiques en associant le nombre 1 pour "vrai", contacteur ouvert, et 0 pour "faux", contacteur fermé.
C'est sur ce principe que fonctionnent encore actuellement les ordinateurs et plus généralement toute technologie "numérique".

Toute donnée traitée actuellement par un système numérique est stockée et manipulée sous la forme de "nombres binaires", c'est-à-dire sous la forme de suites de "0" et de "1".
La représentation physique d'une telle information binaire peut en effet se faire naturellement par tout système à deux états:

des aspérités géométriques sur une surface (CD ...): un creux correspond à un 0 tandis qu'un 1 correspond à un 0;
un signal électrique: au delà d'un certain seuil on considère qu'on est face à un 1, en decà c'est un 0;
un système magnétique (bandes magnétiques, cassettes, ...): le support peut être magnétisé localement (enregistrement de données), puis l'orientation de ces champs magnétiques peut être observé (lecture des données).

On appelle bit un tel nombre, qui signifie binary digit, ou encore chiffre binaire. Un bit correspond à la plus petite unité d'information que peut manipuler un système numérique.

Avec un bit, on peut coder 2 nombres: 0 et 1
bits	Valeur décimale
0	0
1	1

Avec 2 bits, on peut coder 2² = 4
bits	Valeur décimale
00	0
01	1
10	2
11	3

Avec 3 bits, on peut coder 2³ = 8
bits	Valeur décimale
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

D'une manière générale, avec n octets, on peut coder 2ⁿ nombres ou caractères différents.

Un octet, en anglais byte, noté B (attention à la majuscule, à distinguer de la notation b: bit), est une unité d'information composée de 8 bits.
Les multiples classiques, "kilo", "méga", "giga", "peta", ... , peuvent aussi être appliqués. Il faut cependant noter que, appliqués à des octets, ces multiples ne représentent pas des multiples de 10 (ce qui est le cas pour la base naturelle des nombres décimaux), mais un multiple de 2¹⁰ = 1024. Cette utilisation est en toute rigueur erronée, dans le système international: les multiples désignant des puissances de 10 et non de 2, mais, sûrement car l'ordre de grandeur reste le même, l'usage courant l'a conservée.

1 ko, ou 1 kilo octets, représente donc 2¹⁰ = 1024 ≃ 10³ octets.
1 Mo, ou 1 méga octets, représente 2²⁰ = 1 048 576 ≃ 10⁶ octets.
1 Go, ou 1 giga octets, représente 2³⁰ = 1 073 741 824 ≃ 10⁹ octets.
1 to, ou 1 téra octets, représente 2⁴⁰ = 1 099 511 627 776 ≃ 10¹² octets.
1 Po, ou 1 péta octets, représente 2⁵⁰ = 1 125 899 906 842 624 ≃ 10¹⁵ octets.
et ainsi de suite pour les autres multiples ...

Codage binaire d'un nombre

De nombreuses manières permettent de coder un nombre réel sous forme d'une suite binaire.
Il faut tout d'abord bien garder en tête que si un nombre réel peut avoir un nombre infini de décimales (c'est le cas de π, 2, 1/3, … ), et quelle que soit la méthode de codage utilisée, seul un nombre fini, et fixé à l'avance par le type de codage, de ses décimales peut-être codé et stocké par un système numérique.
Les méthodes de codage binaire les plus courantes sont les écritures en simple précision et double précision. L'écriture en simple précision requiert 32 bits pour coder un nombre, tandis que la double précision nécessite 64 bits.
La forme simple précision sur 32 bits est actuellement encore la plus utilisée, quoique les technologies numériques les plus récentes et les plus gourmandes en calcul (les applications graphiques et jeux vidéo entre autres) commence à exploiter les précisions du 64 bits. Le codage sur un nombre plus élevé de bits augmente bien sûr la précision des calculs, mais nécessite bien sûr en contrepartie des capacités en mémoires et en puissance de calcul (puissance des processeurs) accrues.

D'une manière générale, un nombre peut s'écrire sous la forme:

Nombre = (Signe) Mantisse × Base^Exposant

Par exemple, en écriture scientifique, la base utilisée est 10 et la mantisse est un nombre réel positif strictement inférieur à 10.
Par exemple,

1023,432 = + 1,023432 × 10⁴³

−0,0045112 = − 4,5112.10⁻³

Dans l'écriture binaire, la base utilisée est généralement 2, au lieu de 10 pour l'écriture scientifique. Les nombres sont donc représentés sous la forme :

Nombre = (Signe) Mantisse × 2^Exposant

Les codages en simple et double précision utilisent cette forme.
Simple précision: Le codage s'effectue sur 32 bits, en utilisant:

1 bit pour le signe: 0 pour le signe positif et 1 pour un signe négatif
8 bits pour l'exposant: l'exposant peut prendre 2⁸ = 256 valeurs, soit les nombres entiers de −127 à 128
23 bits pour la mantisse

En simple précision le plus petit nombre utilisable est ε = 2⁻¹²⁷ ≃ 5,8.10⁻³⁹ et le plus grand est 2¹²⁸ ≃ 3,4.10³⁸.
Ceci signifie entre autres, que deux nombres donc l'écart est inférieur à ε seront codés de la même façon, et donc, numériquement parlant, seront considérés comme étant égaux.

Double précision Le codage s'effectue sur 64 bits, avec:

1 bit pour le signe
11 bits pour l'exposant: l'exposant peut prendre 2¹¹ = 2048 valeurs, soit les nombres entiers de −1023 à 1024
52 bits pour la mantisse

Numérisation d'un signal

Un signal analogique est un signal réel. La majoritée des signaux ou informations que l'on perçoit dans notre environnement est analogique: les sons qui parviennent jusqu'à notre oreille, la lumière qui excite les cellules photosensibles de notre rétine,
Mathématiquement, c'est une fonction à valeurs réelles, dont la variable est en général le temps est peut prendre toutes les valeurs réelles dans un intervalle donné.
Pour numériser, c'est-à-dire représenter sous la forme d'un ensemble de nombres stockables et manipulables par un système informatique, il a là deux difficultés:

la variable peut prendre une infinité de valeurs: seulement un certain nombre fini de telles valeurs peut être traîté par un ordinateur (ou tout autre système numérique.
la fonction, ou le signal, peut prendre aussi à chaque instant une infinité de valeurs différentes. Là aussi, un travail est nécessaire pour traîter informatiquement ces données.

La réponse au premier point consiste à échantillonner le signal. On ne considère dans toute l'étendue du signal que les valeurs prises à un certains nombres d'instants précis.
Dans un second temps, on quantifie les valeurs du signal à ces instants choisis; il s'agit de représenter, sous forme binaire le plus généralement, les valeurs du signal.

Ce sont les deux étapes incontournables de toute méthode de numérisation (sans parler des difficultés liées à l'acquisition même du signal original): Echantillonnage - Quantification

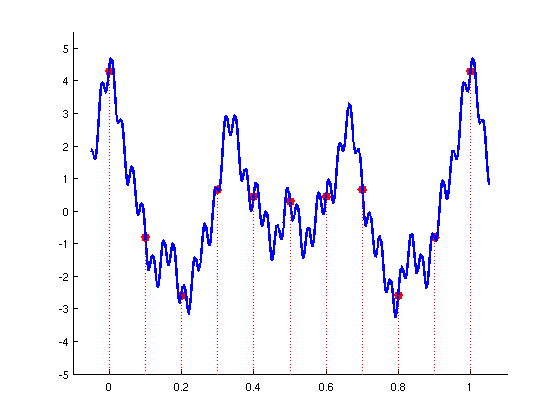
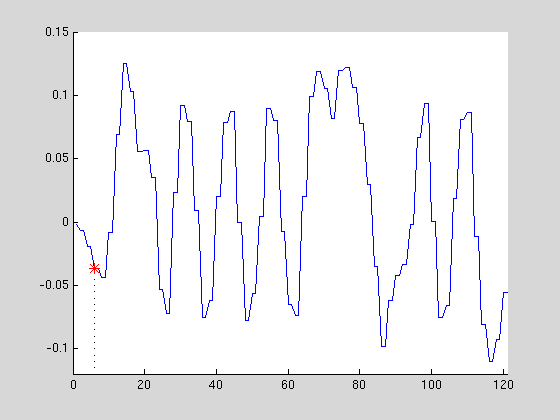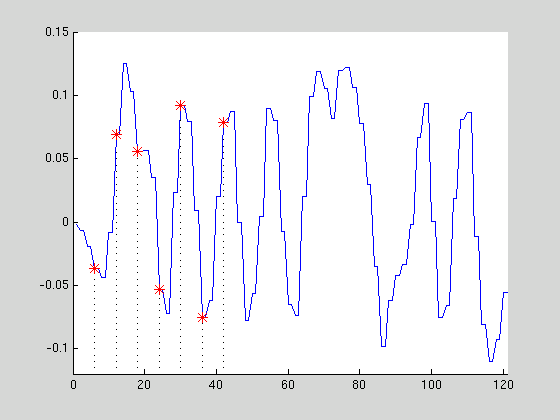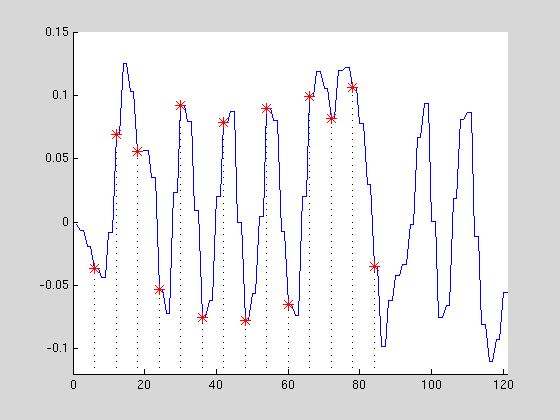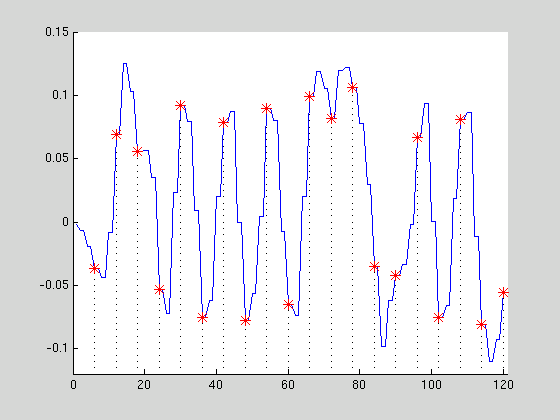
Le signal analogique (ci-dessous en bleu) est échantillonné à intervalles réguliers.
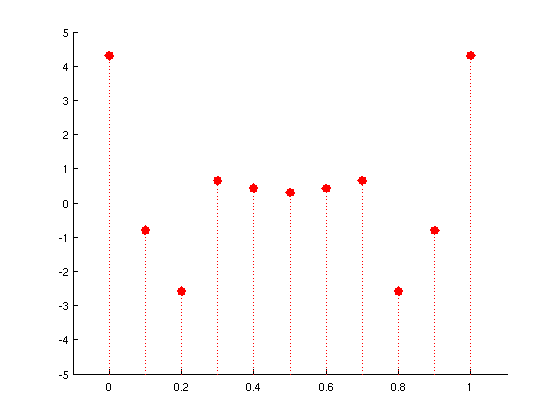
Seules les valeurs prélevées sont conservées (rouge).

Ici, le signal numérique est alors: [ -0,0371 0,0691 0,0558 -0,0533 ... ]
Chaque valeur est ensuite quantifiée, c'est-à-dire convertie sous un format numérique (binaire en général). Numérisation d'un signal analogique

Un point important à noter ici est que, suivant la capacité choisie pour représenter les valeurs prises par le signal analogique d'origine (sur 8 bits, 16 bits , ... ) des valeurs proches peuvent être représentées de la même façon, c'est-à-dire considérées comme égales.
Les nivaux du signal original sont donc lissées. Par exemple, deux sons d'amplitude très légèrement différentes sont représentés, et donc restitué par la suite à l'utilisateur de manière strictement identique.
Ce phénomène est un des inconvénients principalement pointé du doigt par exemple dans le cas de signaux sonores (et musicaux) et de leur numérisation et compression selon le format MP3.

Reconstruction du signal original après numérisation

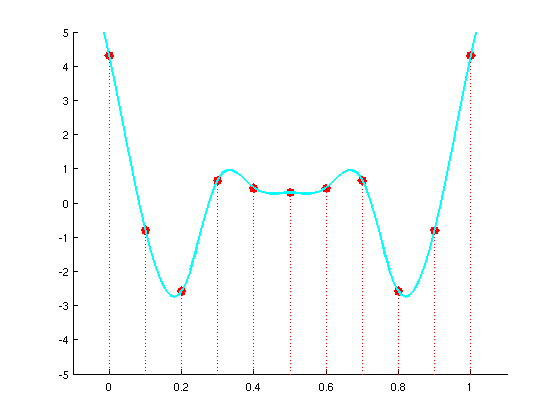
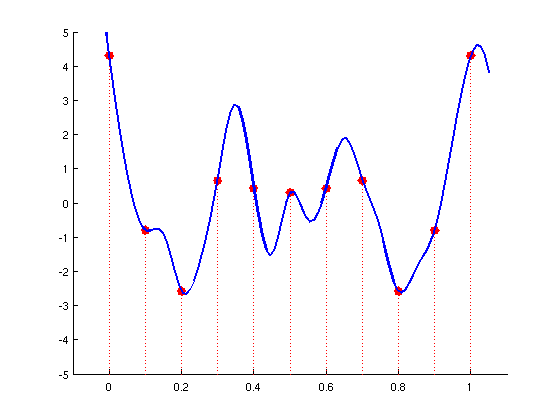
Une question importante se pose suite à la numérisation d'un signal:

est-on capable, à partir des seuls échantillons numérisés de notre signal original, de reconstruire correctement le signal (analogique) original ?

Cette question est primordiale dans les applications les plus courantes.
On peut citer par exemple, pour illustrer cette problématique, l'utilisation de méthodes numériques dans le domaine du traitement de signaux sonores. La chaîne globale comporte deux étapes principales. La première effectue une conversion analogique / numérique, telle que détaillée ci-dessus, qui permet de numériser le ou les sons originaux. Une fois numérisé, le signal peut-être entre autre stocké sur un support adéquat (CD, disque dur, mémoire d'un lecteur MP3, ...).
La dernière étape consiste alors à restituer un signal audible à l'autilisateur, c'est-à-dire à transformer cet ensemble de données numériques (suite d'éléments binaires) en un son perceptible par l'utilisateur.
Bien sûr, et c'est là la moindre des choses, on souhaite que le son perçu par l'utilisateur soit bien celui qu'il aurait entendu directement sans ce traitement numérique.


Un signal (par exemple sonore, un bruit quelconque, un morceau de musique, ...) échantillonné et numérisé (figure de gauche). Seules les valeurs aux instants échantillonnés sont stockées (figure de droite).

Chacun des trois signaux ci-dessus a les mêmes échantillons que le signal original sans pour autant "concorder" avec celui-ci. Le son restitué par chacune de ces trois reconstructions différera de toute évidence du son original enregistré numériquement.

Shannon, mathématicien et informaticien (avant l'heure !) a répondu à cette question en précisant les conditions à respecter pour que la reconstruction soit exacte.
Les hypothèses qui doivent être faites, les conditions à respecter, sont à chercher dans le domaine spectral, c'est-à-dire à rechercher dans le contenu fréquentiel du signal.
La théorie de Fourier donne les outils de compréhension et d'anlayse nécessaires à cette étude et à la réponse fournie par Shannon.