Devoir de maths corrigé, Dérivées et produit scalaire
Première générale, spécialité mathématiques
Devoir de mathématiques, et corrigé, posé en spé maths, première générale, année scolaire 2023/2024
Exercice 1: Variation d'une fonction
Dresser le tableau de variation de la fonction 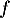 définie par
définie par 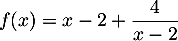 .
.
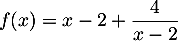 .
.
On a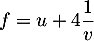 , d'où
, d'où 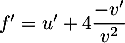 ,
soit
,
soit
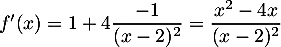
Le numérateur et un trinôme du second degré qui admet deux racines: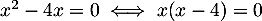 donc
donc 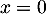 et
et 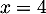 .
.
Le dénominateur s'annule en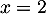 qui est donc une valeur interdite.
qui est donc une valeur interdite.
![\[\begin{tabular}{|c|ccccccccc|}\hline
$x$ & $-\infty$ && 0 && 2 && 4 && $+\infty$ \\\hline
$x^2-4x$ && $+$ &\zb& $-$ &$|$ & $-$ &\zb & $+$ & \\\hline
$(x-2)^2$ && $+$ &$|$& $+$ &\zb& $+$ &$|$ & $+$ & \\\hline
$f'(x)$ && $+$ &\zb& $-$ & & $-$ &\zb & $+$ & \\\hline
&&&&&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\psline(0,-.6)(0,1.3)\,\psline(0,-.6)(0,1.3)&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exvariation_c/9.png)
Cacher la correction
Correction exercice 1
On a
Le numérateur et un trinôme du second degré qui admet deux racines:
Le dénominateur s'annule en
![\[\begin{tabular}{|c|ccccccccc|}\hline
$x$ & $-\infty$ && 0 && 2 && 4 && $+\infty$ \\\hline
$x^2-4x$ && $+$ &\zb& $-$ &$|$ & $-$ &\zb & $+$ & \\\hline
$(x-2)^2$ && $+$ &$|$& $+$ &\zb& $+$ &$|$ & $+$ & \\\hline
$f'(x)$ && $+$ &\zb& $-$ & & $-$ &\zb & $+$ & \\\hline
&&&&&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\psline(0,-.6)(0,1.3)\,\psline(0,-.6)(0,1.3)&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exvariation_c/9.png)
Cacher la correction
Exercice 2: Expressions avec exponentielles à simplifiées
Exercice 3: Réunion et intersection: gâteaux à la crème et/ou aux fruits
Dans une patisserie, il reste 60 petits gâteaux.
La patissière m'informe que parmi ces gâteaux restants,
45 gâteaux sont à base de crème, 12 contiennent des fruits
et que 7 ne contiennent ni crème ni fruits.
Comme je suis pressé et affamé, et que la vitrine ne me semble pas
très ordonnée, je désigne au hasard un gâteau.
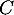 : "à la crème"
: "à la crème"
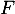 : "avec des fruits"
: "avec des fruits"
Cacher la correction
- Donner la probabilité que mon gâteau soit à la crème mais sans fruits.
- Avant de commencer à manger mon gâteau, je m'aperçois qu'il est aux fruits. Quelle est la probabilité qu'il contienne de la crème ?
Correction exercice 3
Avec un diagramme:  |
Avec un tableau: 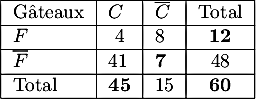 |
Cacher la correction
Exercice 4: Probabilités conditionnelles: Efficacité de stages de révision dans une université
Des étudiants sont inscrits en L1 dans une université.
À l'approche des examens, un stage de révision est organisé. L'expérience montre que 3/4 des étudiants ayant suivi le stage de révision réussissent leurs examens et 1/3 des étudiants n'ayant pas suivi le stage ne réussissent pas leurs examens.
On sait de plus que 20% des étudiants de L1 suivent le stage de révision.
On choisit un étudiant au hasard et on considère les évènements : A : « l'étudiant a suivi le stage de révision» et B : « l'étudiant a réussi ses examens».
Cacher la correction
On choisit un étudiant au hasard et on considère les évènements : A : « l'étudiant a suivi le stage de révision» et B : « l'étudiant a réussi ses examens».
- Construire un arbre de probabilité traduisant la situation étudiée.
- Si l'étudiant choisi a suivi le stage, quelle est la probabilité qu'il n'ait pas réussi ses examens ?
- Quelle est la probabilité que l'étudiant choisi ait suivi le stage et réussi ses examens ?
- Quelle est la probabilité que l'étudiant choisi ait réussi ses examens ?
- Sachant que l'étudiant choisi a réussi ses examens, quelle est la probabilité qu'il ait suivi le stage ?
- (Bonus) L'université trouve que les résultats aux examens de L1 sont trop faibles et aimerait inciter plus d'étudiants à s'inscrire au stage de révision afin qu'au moins 70% des étudiants de L1 réussissent leurs examens. Sachant qu’il y a 300 étudiants inscrits en L1, combien de places faudra-t-il prévoir au minimum lors du stage pour espérer atteindre cet objectif ?
Correction exercice 4
-
![\[\psset{xunit=1cm,yunit=.6cm}
\begin{pspicture}(-2,-3)(5,2.6)
\psline(0,0)(1.5,1.5)\rput(1.75,1.5){$A$}\rput(.7,1.3){$20\%$}
\psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$B$}\rput(2.7,2.3){$3/4$}
\psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{B}$}\rput(2.7,.6){$1/4$}
\psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$\overline{A}$}\rput(.7,-1.3){$80\%$}
\psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$B$}\rput(2.7,-.6){$2/3$}
\psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{B}$}\rput(2.7,-2.4){$1/3$}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap7/exconditionnelles_c/1.png)
- Sachant que l'étudiant choisi a suivi le stage, la probabilité qu'il n'ait pas réussi ses examens est déjà inscrite dans l'arbre
![\[P_A(\overline{B})=\dfrac14\]](/Generateur-Devoirs/1S/Chap7/exconditionnelles_c/2.png)
- La probabilité que l'étudiant choisi ait suivi le stage et réussi ses examens est
![\[P(A\cap B)=20\%\tm\dfrac34=15\%\]](/Generateur-Devoirs/1S/Chap7/exconditionnelles_c/3.png)
- La probabilité que l'étudiant choisi ait réussi ses examens est, d'après la formule des probabilités totales,
![\[P(B)=20\%\tm\dfrac34+80\%\tm\dfrac23\simeq0,68\]](/Generateur-Devoirs/1S/Chap7/exconditionnelles_c/4.png)
- Sachant que l'étudiant choisi a réussi ses examens, la probabilité qu'il ait suivi le stage est
![\[P_B(A)=\dfrac{P(A\cap B)}{P(B)}\simeq\dfrac{15\%}{68\%}\simeq0,22=22\%\]](/Generateur-Devoirs/1S/Chap7/exconditionnelles_c/5.png)
- On note
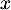 le nombre de places au stage, et on a alors l'arbre
le nombre de places au stage, et on a alors l'arbre
![\[\psset{xunit=1cm,yunit=.6cm}
\begin{pspicture}(-2,-3)(5,2.6)
\psline(0,0)(1.5,1.5)\rput(1.75,1.5){$A$}\rput(.7,1.3){$\frac{x}{300}$}
\psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$B$}\rput(2.7,2.3){$3/4$}
\psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{B}$}\rput(2.7,.6){$1/4$}
\psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$\overline{A}$}\rput(.4,-1.3){$1-\frac{x}{300}$}
\psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$B$}\rput(2.7,-.6){$2/3$}
\psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{B}$}\rput(2.7,-2.4){$1/3$}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap7/exconditionnelles_c/7.png)
On veut maintenant que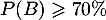 , avec
, avec
![\[P(B)=\dfrac{x}{300}\tm\dfrac34+\lp1-\dfrac{x}{300}\rp\dfrac23
=\dfrac1{12}\tm\dfrac{x}{300}+\dfrac23\]](/Generateur-Devoirs/1S/Chap7/exconditionnelles_c/9.png)
et donc
![\[P(B)\geqslant70\%
\iff\dfrac1{12}\tm\dfrac{x}{300}+\dfrac23\geqslant70\%
\iff x\geqslant300\tm12\lp70\%-\dfrac23\rp=120
\]](/Generateur-Devoirs/1S/Chap7/exconditionnelles_c/10.png)
Il faudra donc pévoir 120 places pour arriver à ce taux de réussite.
Cacher la correction
Quelques autres devoirs
second degré (équation et inéquation, tableau de signe). Dérivabilité d'une fonction en un point: taux d'accroissement et nombre dérivé (calcul et lecture graphique)
fonctions dérivées, étude de fonction et position relative de deux courbes
dérivées et étude de fonction. Angles en radians sur le cercle trigonométrique et en mesure principale
Géométrie avec le produit scalaire, projeté orthogonal et calcul d'un angle et droites tangentes à une parabole perpendiculaires
Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
Quelques exercices corrigés
Exercices corrigés
Cours: définition graphique du nombre dérivé
Exercices corrigés
Calcul du nombre dérivé et tangente
Exercices corrigés
Calculs de dérivées
Exercices corrigés
Calculs de fonctions dérivées
Exercices corrigés
Fonctions dérivées
Voir aussi: