Probabilités conditionnelles
Probabilités conditionnelles, indépendance et arbre de probabilité
Rappels, échauffement …
Exercice 1: probabilités de l'union et de l'intersection
On considère deux événements A et B.
On donne les probabilités: P(A) = 0,75, P(B) = 0,2 et P(A∩B) = 0,1.
- Reproduire et compléter le diagramme de Venn suivant.
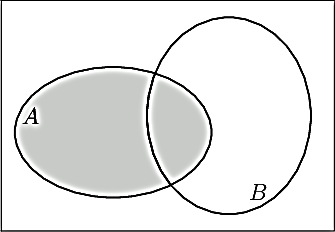
- Donner les probabilités P(), P(A∪B) et P(A∩).
Correction
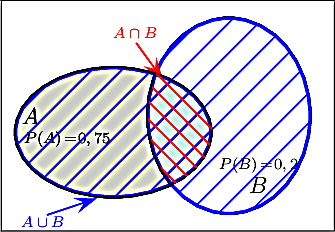
- On a les probabilités:
- P() = 1 − P(A) = 0,25
- P(A∪B) = P(A) + P(B) − P(A∩B) = 0,85
- A∩ est l'ensemble A sans la partie B, et on a P(A∩) = P(A) − P(A∩B) = 0,1
Exercice 2: des vélos et/ou des rollers
Une étude dans une grande ville a donné les résultats suivants:
73% des personnes ont un velo,
19% ont des rollers et 17% possèdent les deux.
On note R l'événement: "la personne a des rollers" et V: "la personne a un vélo".
- Compléter le tableau:
V Total R Total 100% - On désigne une personne au hasard dans l'annuaire de la ville.
- Déterminer la probabilité que cette personne ait soit un velo soit des rollers.
- Déterminer la probabilité que cette personne n'ait ni velo ni roller ?
- Quelle est la probabilité que cette personne ait des rollers mais pas de velo?
- La personne contactée affirme tout de suite posséder un vélo. Quelle est la probabilité qu'elle ait alors aussi des rollers ?
- Je travaille dans un magasin de cycle. Un potentiel client entre dans mon magasin en rollers. Quelle est la probabilité qu'il ait déjà un vélo ?
Correction
- On reporte (en rouge) les données directement fournies par l'énoncé. Esuite, on complète facilement les autres valeurs (en bleu), par soustraction, complément, ...
V Total R 17% 2% 19% 56% 25% 81% Total 73% 27% 100% - En utilisant maintenant directement les valeurs dans ce tableau de probabilité, on a:
- P(R∪V) = 17%+2%+56%=75%
- P(∪) = 25%
- P(∩V) = 56%
- On sait déjà que la personne contactée possède un vélo. La probabilité qu'elle ait alors aussi un roller est alors c'est-à-dire que une probabilité de 17% sur les 73% qui possèdent un vélo, soit la probabilité P = 17%73% ≃ 0,23 = 23%
- De même que dans la question précédente, la probabilité qu'il ait un vélo est de 17% sur les 19% qui ont des rollers, soit la probabilité P = 17%19% ≃ 0,89 = 89%
Exercice 3: Pile ou Face, plusieurs fois
- Je lance deux fois de suite une pièce bien équilibrée.
Représenter la situation à l'aide d'un arbre.
Quelle est la probabilité d'obtenir 2 fois Pile exactement ? - Même question que précédemment mais en lançant cette fois trois de suite cette pièce.
Correction

La probabilité d'obtenir deux fois Pile est donc p = 12 × 12 = 14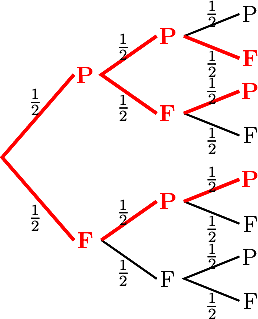
Il y a trois façon d'obtenir 2 fois Pile, chacun avec la même probabilité.
La probabilité est donc de p = 3 × 12 × 12 × 12 = 38
Probabilités conditionnelles
Définition
Définition: probabilité conditionnelle
Soit A et B deux événements, avec P(A)≠=0.
La probabilité conditionnelle de l'événement B sachant A, notée PA(B), est définie par
PA(B) =
P(A∩B)P(A)
On exprime alors, de manière équivalente, la probabilité de l'intersection:
P(A∩B) = P(A)×PA(B)
Exercice 4
La probabilité qu'un jeune réussisse l'examen du permis de conduire
l'année de ses 18 ans est de 0,625 et celle qu'il soit reçu au
baccalauréat cette même année est de 0,82.
De plus, la probabilité d'être à la fois reçu au baccalauréat et à l'examen du permis de conduire la même année est de 0,56.
- Calculer la probabilité qu'un jeune soit reçu à au moins un des deux examens.
- En déduire la probabilité qu'il ne soit reçu à aucun des deux examens.
- Déterminer la probabilité qu'un jeune réussisse au baccalauréat sachant qu'il a déjà eu son permis la même année.
On note les événements: C: "le jeune est reçu au permis de conduire" et B:"le jeune est reçu au baccalauréat".
- On cherche la probabilité de la réunion:
P(C∪B) = P(C) + P(B) − P(C∩B) = 0,625 + 0,82 − 0,56 = 0,885 = 88,5%
- "n'être reçu a aucun examen" est l'événement ∩ et qui l'événement contraire du précédent, et donc de probabilité
P(∩) = 1 − 0,885 = 0,115 = 11,5%
- La probabilité recherchée est une probabilité conditionnelle:
PC(B) = P(C∩B)P(C) = 0,560,625 = 0,896 = 89,6%
Événements indépendants
Définition: Événements indépendants
On dit que deux événements A et B sont indépendants lorsque
PA(B) = P(B)
"Savoir que l'événement A est arrivé ne change pas la probabilité de l'événement B".
Remarques:
- Si A et B sont indépendants, on a aussi PB(A) = P(A).
- Ne pas confondre indépendance et incompatibilité: A et B sont incompatibles, ou disjoints, lorsque A∩B = ∅ (et dans ce cas alors, on a d'ailleurs PA(B) = 0)
Exercice 5
Dans un jeu de 52 cartes, on tire au hasard une carte et on considère les événements:
- A: "la carte tirée est un As"
- B: "la carte tirée est un pique"
- C: "la carte tirée est une figure (valet, dame, roi, ou as)"
- Donner les probabilités de ces trois événements.
- J'ai tiré une carte au hasard et j'ai entr'aperçu que la carte tirée est un pique. Quelle est la probabilité que ce soit un As.
Écrire cette probabilité en utilisant les événements A et B. - J'ai tiré une carte au hasard et j'ai entr'aperçu cette fois que la carte tirée est une figure. Quelle est alors la probabilité que ce soit un As.
Écrire cette probabilité en utilisant les événements A et C. - Que peut-on dire des événements A et B d'une part, et A et C d'autre part ?
- Il y a 4 as dans le jeu, d'où la probabilité
P(A) = 452
= 113
Il y a 13 cartes pique, d'où la probabilité P(B) = 1352 = 14
Enfin, il y a 4×4 figures, d'où la probabilité P(C) = 1652 = 413 - Sachant déjà que la carte est un pique, il n'y a plus que 13 cartes à considérer, et la probabilité que ce soit un as est (il n'y a donc aussi plus qu'un seul as possible) PB(A) = 113
- Sachant cette fois que la carte est une figure, il n'y a plus que 4×4 = 16 cartes à considérer, et la probabilité que ce soit un as est PC(A) = 416 = 14
- Les événements A et B sont indépendants, car
PB(A) = P(A) = 113
Par contre, les événements A et C sont dépendants: connître à l'avance que C est réalisé change la probabilité de l'événement A.
Propriété: évenements indépendants
Les événements A et B sont indépendants si et seulement si
P(A∩B) = P(A)×P(B)
Si A et B sont indépendants, alors et B sont aussi indépendants (et donc et ).
Exercice 6
Les probabilités des événements indépendants A et B sont
P(A) = 0,8 et P(B) = 0,5.
Quelle est la probabilité P(A∪B) ?
Les événements A et B sont indépendants, d'où
P(A∩B) = P(A)×P(B) = 0,8×0,5 = 0,4
et alors
P(A∪B) = P(A) + P(B) − P(A∩B) = 0,8 + 0,5 − 0,4 = 0,7
Exercice 7
On considère deux événements A et B tels que
P(A) = 0,8, P(B) = 0,35 et P(A∩B) = 0,28.
- Montrer que A et B sont indépendants.
- Calculer P(A∪B) puis P(∩B).
- Ces événements sont indépendants car
P(A)×P(B) = 0,8×0,35 = 0,28 = P(A∩B)
-
P(A∪B) = P(A) + P(B) − P(A∩B) = 0,8 + 0,35 − 0,28 = 0,87etP(∩B) = P(B) − P(A∩B) = 0,35 − 0,28 = 0,07
Exercice 8
Deux événements sont indépendants et ont, indépendamment donc, la même probabilité. De plus, il y a une chance sur quatre que ces deux événements se réalisent simultanément.
Quelle est la probabilité de ces événements ?
On note A et B ces deux événements, et on a alors
P(A) = P(B)
ainsi que P(A∩B) = 14.
On sait de plus que ces déux événements sont indépendants, et donc que P(A∩B) = P(A)×P(B)
On a alors
On sait de plus que ces déux événements sont indépendants, et donc que P(A∩B) = P(A)×P(B)
On a alors
14 = P(A∩B) = P(A)×P(B) = P(A)2
On en déduit, comme P(A)≥0, que
P(A) =
14
=
14
=
12
Arbre de probabilité
Arbre de probabilité
- Règle 1
- La somme des probabilités issues d'un nœud est égale à 1.
- Règle 2: Probabilités conditionnelles
- Sur chaque branche, on inscrit la probabilité conditionnelle: probabilité de l'événement de droite sachant celui de gauche.
- Règle 3
- Un chemin correspond à l'intersection des événements.
Sa probabilité est le produit des probabilités. - Règle 4: Probabilités totales
- La probabilité d'un événement est la somme des probabilités des chemins qui mènent à cet événement.
Exercice 9
Une branche présente 10 fleurs: 2 blanches et 8 roses.
On cueille, successivement et au hasard, 3 fleurs.
- Représenter la situation par un arbe pondéré.
- Quelle est la probabilité d'avoir 3 fleurs roses ?
Quelle est la probabilité d'avoir les 2 fleurs blanches ?
-
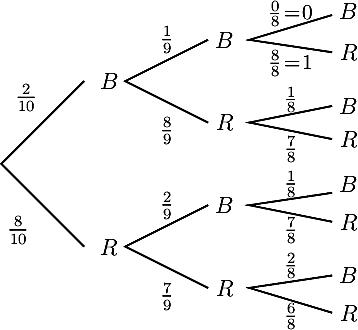
- En utilisant l'arbre de probabilité précédent, on a maintenant la probabilité d'avoir 3 fleurs roses:
p = 810 ×79 ×68 = 715Il y a 3 chemins pour lesquels on obtient 2 fleurs blanches (et donc forcément 1 rose):p = 210 ×19 ×1 + 210 ×89 ×18 + 810 ×29 ×18 = 345
Exercice 10
On considère une expérience aléatoire modélisée par l'arbre suivant.

- Compléter cet arbre.
- Déterminer P(A∩B) et P(B).
- Déterminer PA(B) et PB(A).
- On complète simplement cet arbre en utilisant la 1ère règle.
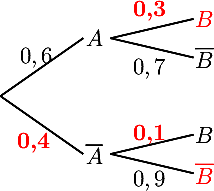
- En utilisant maintenant la 3ème règle, on a
P(A∩B) = 0,6 × 0,3 = 0,18puis en utilisant la formule des probabilités totales, 4ème règle,P(B) = 0,6 × 0,3 + 0,4 × 0,1 = 0,22
- La première probabilité conditionnelle est directement dans l'arbre:
PA(B) = 0,3tandis que la deuxième n'est pas directement dans notre arbre. On revient alors à la définition de la probabilité conditionnellePB(A) = P(A∩B)P(B)soit, avec les résultats des questions précédentes,PB(A) = 0,180,22 ≃ 0,82
Exercice 11
Une expérience aléatoire est représentée par l'arbre pondéré suivant.
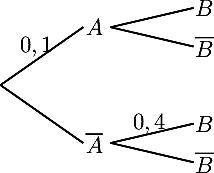
On sait de plus que P(B) = 0,39.
- Déterminer la probabilité de B sachant A.
- Calculer la probabilité de l'événement A∩B.
- Calculer la probabilité de A sachant B.
- On complète facilement dans l'arbre la branche P() = 0,9,
La probabilité recherchée est alors celle sur la branche du haut, pour laquelle on peut utiliser la probabilité donnée dans l'énoncé, et avec la formule des probabilités totales (règle 4)P(B) = P(A)×PA(B) + P()×P(B)soit0,39 = 0,1×PA(B) + 0,9×0,4d'oùPA(B) = 0,39 − 0,9×0,40,1 = 0,3 - On calcule alors la probabilité de l'intersection recherchée:
P(A∩B) = P(A)×PA(B) = 0,1×0,3 = 0,03.
- On calcule maintenant la probabilité conditionnelle
PB(A) = P(A∩B)P(B) = 0,030,39 ≃ 0,077de A sachant B.
Exercice 12
Tous les élèves d'une promotion ont passé un test de certification en anglais.
- 80% ont réussi le test.
- Parmi ceux qui ont réussi le test, 95% le passaient pour la 1ère fois.
- Parmi ceux qui ont échoué au test, 2% le passaient pour la 1ère fois.
- Traduire l'énoncé en termes de probabilité et dresser un arbre pondéré décrivant la situation.
- Calculer la probabilité qu'un élève choisi au hasard ait passé le test pour la 1ère fois et l'ait réussi.
- Déterminer la probabilité qu'un élève choisi au hasard ait passé plusieurs fois le test.
- On choisit au hasard un élève ayant passé plusieurs fois le test. Quelle est la probabilité qu'il ait réussi ?
- En termes de probabilités, on a dans l'énoncé
P(R) = 80%,
PR(F) = 95%, et
P() = 2%.
On peut alors dresser l'arbre de probabilité: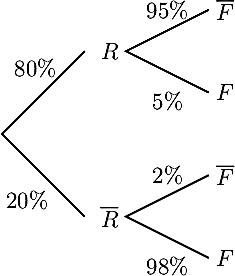
- On cherche la probabilité de l'intersection
P(R∩)= 80%×95% = 76%
- Avec la formule des probabilités totales (règle 4), on a
P(F) = 80%×5% + 20%×98% = 23,60%
- On cherche la probabilité conditionnelle:
PF(R) = P(R∩F)P(F) = 80%×5%23,60% ≃ 16,95%
Exercice 13: Formule de Bayes.
Pour A et B deux événements de probabilités non nulles.
Représenter la situation par un arbre et montrer la formule et montrer la formule
PB(A) = PA(B)
P(A)P(B)
puis la la formule
PB(A) =
PA(B)P(A)PA(B)×P(A) + P(B)×P()
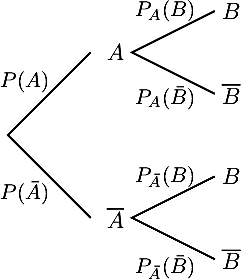
On a, par définition de la probabilité conditionnelle
PB(A) =
P(A∩B)P(B)
et de même, dans "l'autre sens"
PA(B) =
P(A∩B)P(A)
⇔ P(A∩B) = PA(B)×P(A)
En remplaçant cette expression de l'intersection dans la probabilité conditionnelle précédente, on obtient directement la formule de Bayes souhaitée.
Pour obtenir la 2ème formule, il faut juste maintenant changer le dénominateur de celle obtenue précédemment. C'est la formule des probabilités totales (règle 4) qui s'écrit avec notre arbre
P(A) = P(A)×PA(B) + P()×P(B)
et on obtient donc la 2ème formule demandée en remplaçant cette expression dans le dénominateur de la formule précédente.
Exercice 14: Applications de la formule de Bayes
- On dispose de 100 pièces de monnaie.
Une pièce sur quatre est truquée.
Une pièce truquée indique Pile avec une probabilité de
45
On choisit au hasard une pièce parmi les 100, on la lance et on obtient Pile. Quelle est la probabilité qu'il s'agisse d'une pièce truquée ? - Dans une population, une personne sur quatre triche.
Lorsqu'on fait tirer une carte d'un jeu de 52 cartes à un tricheur, il tire à tous les coups un as.
α) On demande à une personne au hasard de tirer une carte, quelle est la probabilité qu'un as soit tiré ?
β Un as a été tiré. Quelle est la probabilité que j'ai eu affaire à un tricheur ? - Peur des coupures de courant ?
Le système électrique dans un bâtiment est quasi-certainement endommagé lors d'un incendie; plus précisément, il y a 99 chances sur 100 pour que le courant soit coupé lors d'un incendie.
Hors incendie, les normes électriques permettent d'avoir des systèmes assez fiables et la probabilité d'une coupure de courant reste de l'ordre d'une chance sur 1000.
Enfin, statistiquement, un incendie se déclare tous les 3 ou 4 ans, c'est-à-dire que, plus précisément, un incendie survient un jour donné avec une probabilité de 10−3.
Les lumières viennent de s'éteindre brusquement ! Quelle est la probabilité pour que se soit un incendie ?
Exercice 15: Voitures rouges volées
Une étude statistique donne les valeurs: 20% des voitures sont rouges, 1% des voitures rouges se font voler.
Pour les autres voitures, toutes couleurs confondues, le double se font voler, soit 2%.
- Représenter la situation par un arbre.
- Quelle est la probabilité qu'une voiture se fasse voler ?
- Un ami m'annonce qu'il vient de se faire voler sa voiture. Quelle est la probabilité que sa voiture (ou plutôt son ancienne voiture, maintenant) ne soit pas rouge ?
- On note les événements: R:"la voiture est rouge" et V:"la voiture est volée".
On dresse alors l'arbre de probabilité:
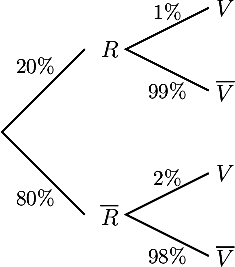
- La probabilité qu'une voiture se fasse voler est, en utilisant la formule des probabilités totales (règle 4)
P(V) = 20%×1% + 80%×2% = 1,8%
- On sait déjà l'événement V et on cherche alors la probabilité conditionnelle:
PV() = P(∩V)P(V) = 80%×2%1,8% ≃ 88,9%
Exercice 16: Test de dépistage
On définit, pour un test de dépistage d'une maladie:
- sa sensibilité: la probabilité qu'il soit positif si la personne est atteinte de la maladie (vrai positif).
- sa spécificité: la probabilité qu'il soit négatif si la personne est indemne de la maladie (vrai négatif).
- sa valeur prédictive positive (ou valeur diagnostique): la probabilité que la personne soit réellement malade si son test est positif.
- sa valeur prédictive négative: la probabilité que la personne n'ait pas la maladie si son test est négatif.
Les valeurs prédictives sont quant à elles des données intéressantes du point de vue de l'usager (patient).
Le fabricant du test fournit les caractéristiques suivantes:
- la probabilité qu'un individu malade ait un test positif est 0,98 (sensiblité du test);
- la probabilité qu'un individu non malade ait un test négatif est 0,99 (spécificité du test).
- On utilise ce test pour dépister une maladie qui touche 30% de la population.
- Dresser un arbre pondéré décrivant la situation.
- Calculer la probabilité de l'événement T.
- Déterminer les valeurs prédictives positive et négative du test.
- Calculer de même les valeurs prédictives positives de ce test pour une maladie qui toucherait 0,1% de la population.
-
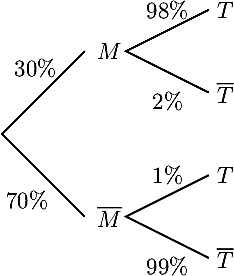
- D'après la formule des probabilités totales (règle 4), on a
P(T) = 30%×98% + 70%×1% = 30,1%
- La valeur prédictives positive est la probabilité
PT(M) = P(M∩T)P(T) = 30%×98%30,1% ≃ 97,67%La valeur prédictives négative est la probabilitéP() = P(∩)P() = 70%×99%100%−30,1% ≃ 99,14%
- On reprend l'arbre avec la nouvelle donnée:
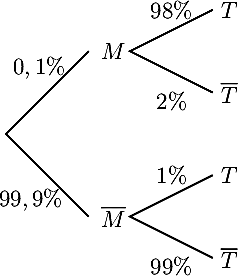
On reprend ensuite les calculs précédents:P(T) = 0,1%×98% + 99,9%×1% ≃ 1,01%puis la valeur prédictives positive:PT(M) = P(M∩T)P(T) = 0,1%×98%1,01% ≃ 9,7%Ainsi, lorsqu'un test est positif, la probabilité que le patient concerné soit effectivement malade est en fait très faible: moins de 1 chance sur 10 ! (tirer à Pile ou Face serait bien plus sûr, avec une probabilité de 1 chance sur 2!).
La valeur prédictives négative est quant à elle:P() = P(∩)P() = 99,9%×99%100%−1,01% ≃ 99,99%et là, si le test est négatif, la probabilité que le patient ne soit effectivement pas malade est très forte.
Exercice 17: Oubli de la fréquence de base
Dans une ville d'un million d'habitants, 100 individus sont fichés dangereux. La mairie installe un système de surveillance algorithmique capable de détecter automatiquement le visage des personnes qui passent dans son champ.
Bien sûr, comme tout système de mesure, celui-ci n'est pas infaillible: on suppose ici que le système est de bonne qualité avec un taux d'erreur de seulement 1%.
Une personne a commis un méfait dans le champ d'une caméra, et l'alarme s'est déclenchée.
Quelle est la probabilité que ce soit effectivement un des délinquants listés ?
Avec le taux d'erreur annoncé, on est tenté de répondre 99%, et 1% d'erreur que ce ne soit pas un délinquant~fiché…
Calculer ces probabilités exactement: à savoir la probabilité, une fois que l'alarme s'est déclenchée, que ce soit par un des délinquants fichés.
Calculer de même la probabilité, sachant que l'alarme s'est déclenchée, que ce soit du fait d'un citoyen non fiché comme délinquant.
Voir aussi, en complément, Oubli de la fréquence de base et exemples d'explication de préjugés
On note les événements D: " l'individu est un délinquant fiché "
A: " l'alarme est déclenchée ".
Il y a 100 individus fichés délinquants sur un million d'habitants, d'où la probabilité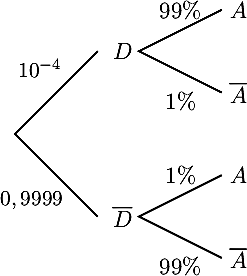
On cherche alors les probabilités PA(D) et PA()
Pour la première, on a
Il y a 100 individus fichés délinquants sur un million d'habitants, d'où la probabilité
P(D) = 100106 = 10−4
et donc aussi
P() = 1 − P(D) = 0,9999
On peut alors dresser l'arbre de probabilité:

On cherche alors les probabilités PA(D) et PA()
Pour la première, on a
PA(D) =
P(D∩A)P(A)
avec, par la formule des probabilités totales
P(A) = 10−4×99% + 0,9999×1% ≃ 0,0101 = 1,01%
et donc
PA(D) ≃
10−4×99%1,01%
≃ 0,98%
et de même
PA() =
P(∩A)P(A)
≃ 0,9999×1%1,01%
≃ 0,99 = 99%
Voir aussi: