Réunion, intersection et contraire
Exercice corrigé - Spécialité maths, première générale
Énoncé
Soit 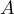 et
et 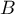 deux événements tels que
deux événements tels que
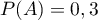 ,
, 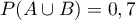 et
et 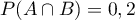 .
.
- Calculer
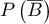 .
.
- Les événements
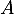 et
et 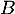 sont-ils indépendants ?
sont-ils indépendants ?
Correction
Correction
-
On a
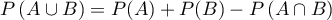
soit aussi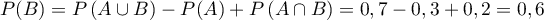 .
.
On a alors,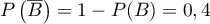 .
.
- On a donc
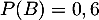 et
et 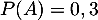 d'où
d'où
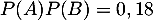 .
.
Or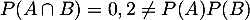 , ce qui montre que les événements
, ce qui montre que les événements 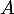 et
et 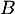 ne sont pas indépendants.
ne sont pas indépendants.
Tag:Probabilités conditionnelles
Voir aussi:
Quelques devoirs
Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
une étude des variations d'une fonction - Calcul de la valeur approchée d'un angle avec le produit scalaire dans un repère - Probabilités conditionnelles et réunion / intersection d'événements
une étude des variations d'une fonction - Calcul de la valeur approchée d'un angle avec le produit scalaire dans un repère - Probabilités conditionnelles et réunion / intersection d'événements
dérivée et sens de variation d'une fonction rationnelle - Calculs algébriques et équations avec exponentielles - Probabilités conditionnelles et arbre de probabilité
équations et inéquations avec exponentielles, variation de fonctions avec exponentielle, probabilités conditionnelle et arbre de probabilité
