Devoir de maths corrigé, Dérivées et produit scalaire
Première générale, spécialité mathématiques
Devoir de mathématiques, et corrigé, posé en spé maths, première générale, année scolaire 2023/2024
Exercice 1: Variation de l'inverse d'un trinome et équation d'une tangente
Dresser le tableau de variation de la fonction 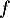 définie par
définie par 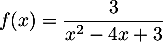 .
.
Soit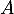 le point de la courbe de
le point de la courbe de 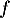 et d'abscisse nulle.
Déterminer les coordonnées de
et d'abscisse nulle.
Déterminer les coordonnées de 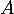 et l'équation de la tangente à la courbe de
et l'équation de la tangente à la courbe de 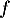 au point
au point 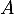 .
.
Soit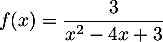 .
On a
.
On a 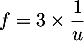 avec
avec 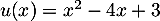 et donc
et donc 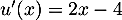 .
.
On trouve alors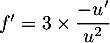 ,
soit
,
soit 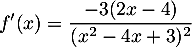
Pour le dénominateur, on a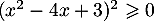 ,
avec le trinôme
,
avec le trinôme 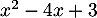 qui a pour discriminant
qui a pour discriminant 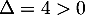 et qui admet donc deux racines réelles distinctes
et qui admet donc deux racines réelles distinctes
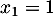 et
et 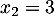 .
.
On dresse alors le tableau de variation:
![\[\begin{tabular}{|c|ccccccccc|}\hline
$x$ & $-\infty$ && 1 && 2 && 3 && $+\infty$ \\\hline
$-3$ && $-$ &$|$ & $-$ &$|$ & $-$ &$|$ & $-$ &\\\hline
$2x-4$ && $-$ &$|$ &$-$ &\zb& $+$ & $|$ & $+$ &\\\hline
$(x^2-4x+3)^2$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} &$+$ &$|$& $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ &\\\hline
$f'(x)$ && $+$ & &$+$ &\zb& $-$ & & $-$ &\\\hline
&&&&&$-3$&&&&\\
$f$&&\Large{$\nearrow$}&\psline(0,-.6)(0,1.3)\,\psline(0,-.6)(0,1.3)&\Large{$\nearrow$}&&\Large{$\searrow$}&\psline(0,-.6)(0,1.3)\,\psline(0,-.6)(0,1.3)&\Large{$\searrow$}&\\
&&&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exvar4_c/12.png)
On a , soit
, soit 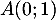 .
La tangente en
.
La tangente en 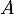 a pour équation
a pour équation
![\[y=f'(0)(x-0)+f(0)=\dfrac43x+1\]](/Generateur-Devoirs/1S/Chap3/exvar4_c/16.png)
Cacher la correction
Soit
Correction exercice 1
Soit
On trouve alors
Pour le dénominateur, on a
On dresse alors le tableau de variation:
![\[\begin{tabular}{|c|ccccccccc|}\hline
$x$ & $-\infty$ && 1 && 2 && 3 && $+\infty$ \\\hline
$-3$ && $-$ &$|$ & $-$ &$|$ & $-$ &$|$ & $-$ &\\\hline
$2x-4$ && $-$ &$|$ &$-$ &\zb& $+$ & $|$ & $+$ &\\\hline
$(x^2-4x+3)^2$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} &$+$ &$|$& $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ &\\\hline
$f'(x)$ && $+$ & &$+$ &\zb& $-$ & & $-$ &\\\hline
&&&&&$-3$&&&&\\
$f$&&\Large{$\nearrow$}&\psline(0,-.6)(0,1.3)\,\psline(0,-.6)(0,1.3)&\Large{$\nearrow$}&&\Large{$\searrow$}&\psline(0,-.6)(0,1.3)\,\psline(0,-.6)(0,1.3)&\Large{$\searrow$}&\\
&&&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/exvar4_c/12.png)
On a
Cacher la correction
Exercice 2: Valeur approchée d'un angle avec le produit scalaire
Dans le plan muni d'un repère orthonormé, soit les points
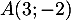 ,
, 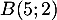 et
et 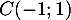 .
.
Donner une valeur de l'angle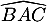 au dixième de degré près.
au dixième de degré près.
Soit les points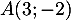 ,
, 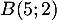 et
et 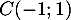 ,
on a donc
,
on a donc 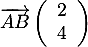 et
et 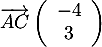
d'où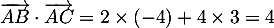
On a aussi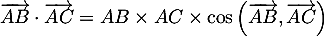 ,
,
avec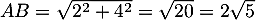 et
et 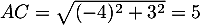 ,
d'où
,
d'où 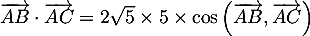 .
.
On a alors, en utilisant la question précédente,
![\[\overrightarrow{AB}\cdot\overrightarrow{AC}=4=2\sqrt5\tm5\tm\cos\lp\overrightarrow{AB},\overrightarrow{AC}\rp\]](/Generateur-Devoirs/1S/Chap6/exangle_c/11.png)
soit aussi
![\[\cos\lp\overrightarrow{AB},\overrightarrow{AC}\rp=\dfrac4{2\sqrt5\tm5}=\dfrac2{5\sqrt5}\]](/Generateur-Devoirs/1S/Chap6/exangle_c/12.png)
Avec l'aide de la caclulatrice, on trouve alors la valeur approché de l'angle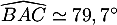
Cacher la correction
Donner une valeur de l'angle
Correction exercice 2
Soit les points
d'où
On a aussi
avec
On a alors, en utilisant la question précédente,
soit aussi
Avec l'aide de la caclulatrice, on trouve alors la valeur approché de l'angle
Cacher la correction
Exercice 3: Probabilités conditionnelles: organisation d'un concert de musique
Un groupe d'élèves d'une classe de première générale veut organiser un concert de musique à l'intérieur du lycée.
Il fait une enquête pour connaître le nombre d'élèves souhaitant assister à ce concert.
450 élèves ont répondu à cette enquête, 180 garçons et 270 filles. 144 filles et 72 garçons sont favorables et souhaitent assister au concert.
Par la suite, on note les événements:
 : « l'élève est un garçon»
: « l'élève est un garçon»
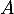 : « l'élève souhaite assister au concert»
: « l'élève souhaite assister au concert»
Cacher la correction
450 élèves ont répondu à cette enquête, 180 garçons et 270 filles. 144 filles et 72 garçons sont favorables et souhaitent assister au concert.
Par la suite, on note les événements:
- On prend la fiche au hasard d'un élève ayant répondu à cette enquête.
Donner les probabilités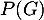 ,
, 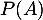 ,
, 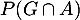 et
et 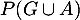 .
.
- Les événements
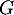 et
et 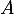 sont-ils indépendants ?
sont-ils indépendants ?
- Calculer la probabilité
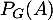 , et interpréter cette probabilité (avec une phrase).
, et interpréter cette probabilité (avec une phrase).
- Au concert, un élève devant moi me dérange. Quelle est la probabilité que ce soit un garçon ?
Correction exercice 3
- On a
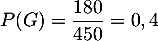 ,
, 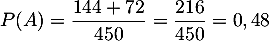 ,
,
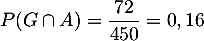 et donc
et donc
![\[P(G\cup A)=P(G)+P(A)-P(G\cap A)=0,72\]](/Generateur-Devoirs/1S/Chap7/exconcert_c/4.png)
- On a
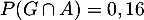 et
et 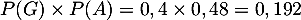 , donc ces événements ne sont pas indépendants.
, donc ces événements ne sont pas indépendants.
-
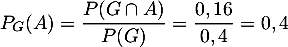 .
.
Ainsi, sachant qu'on parle d'un garçon, la probabilité qu'il souhaite assister au concert est de 40%.
- On cherche la probabilité conditionnelle
![\[P_A(G)=\dfrac{P(A\cap G)}{P(A)}=\dfrac{0,16}{0,48}\simeq0,33\]](/Generateur-Devoirs/1S/Chap7/exconcert_c/8.png)
Cacher la correction
Exercice 4: Réunion et intersection, cartes à puces avec deux défauts
Une entreprise fabrique des cartes à puces. Chaque puce peut présenter deux défauts notés A et B. Une étude statistique montre que 2,8% des puces ont le défaut A, 2,2% des puces ont le défaut B et, heureusement, 95,4% des puces n'ont aucun des deux défauts.
Quelle est la probabilité qu'une puce prélevée au hasard ait les deux défauts ?
(D'après Bac centres étrangers, 9 juin 2021)
On note A et B les événements: "la puce a le défaut A" et "la puce a le défaut B", et l'énoncé se traduit alors par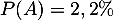 ,
, 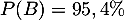 et
et
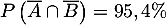 ,
ou encore le diagramme de Venn
,
ou encore le diagramme de Venn
(4,2)(4,-2)(-4,-2)
\rput[l](-3.8,1.6){95,4\%}
\psellipse[fillstyle=solid,,fillcolor=white](-1,0)(1.8,1)
\rput[l](-2.4,.3){A}
\rput[l](-2.4,-.1){2,8\%}
\psellipse[fillstyle=solid,fillcolor=white](1,0)(1.8,1)
\rput[r](2.4,.3){B}
\rput[r](2.4,-.1){2,2\%}
\begin{psclip}{%
\psellipse(-1,0)(1.8,1)}
\psellipse[fillstyle=vlines](1,0)(1.8,1)
\end{psclip}
\psellipse[linestyle=none,fillstyle=solid,fillcolor=white](0.05,0)(.25,.3)
\rput(0,0){\large\bf\red ?}
\end{pspicture}
\]](/Generateur-Devoirs/1S/Chap7/expuces_c/4.png)
En utilisant le diagramme de Venn précédent, on a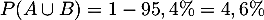 puis
puis
![\[P(A\cap B)=P(A)+P(B)-P(A\cup B)
=2,8\%+2,2\%-4,6\%=0,4\%\]](/Generateur-Devoirs/1S/Chap7/expuces_c/6.png)
La probabilité qu'une puce prélevée au hasard ait les deux défauts est donc de 0,4%.
Cacher la correction
Quelle est la probabilité qu'une puce prélevée au hasard ait les deux défauts ?
Correction exercice 4
(D'après Bac centres étrangers, 9 juin 2021)
On note A et B les événements: "la puce a le défaut A" et "la puce a le défaut B", et l'énoncé se traduit alors par
(4,2)(4,-2)(-4,-2)
\rput[l](-3.8,1.6){95,4\%}
\psellipse[fillstyle=solid,,fillcolor=white](-1,0)(1.8,1)
\rput[l](-2.4,.3){A}
\rput[l](-2.4,-.1){2,8\%}
\psellipse[fillstyle=solid,fillcolor=white](1,0)(1.8,1)
\rput[r](2.4,.3){B}
\rput[r](2.4,-.1){2,2\%}
\begin{psclip}{%
\psellipse(-1,0)(1.8,1)}
\psellipse[fillstyle=vlines](1,0)(1.8,1)
\end{psclip}
\psellipse[linestyle=none,fillstyle=solid,fillcolor=white](0.05,0)(.25,.3)
\rput(0,0){\large\bf\red ?}
\end{pspicture}
\]](/Generateur-Devoirs/1S/Chap7/expuces_c/4.png)
En utilisant le diagramme de Venn précédent, on a
La probabilité qu'une puce prélevée au hasard ait les deux défauts est donc de 0,4%.
Cacher la correction
Quelques autres devoirs
second degré (équation et inéquation, tableau de signe). Dérivabilité d'une fonction en un point: taux d'accroissement et nombre dérivé (calcul et lecture graphique)
fonctions dérivées, étude de fonction et position relative de deux courbes
dérivées et étude de fonction. Angles en radians sur le cercle trigonométrique et en mesure principale
Géométrie avec le produit scalaire, projeté orthogonal et calcul d'un angle et droites tangentes à une parabole perpendiculaires
Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
Quelques exercices corrigés
Exercices corrigés
Cours: définition graphique du nombre dérivé
Exercices corrigés
Calcul du nombre dérivé et tangente
Exercices corrigés
Calculs de dérivées
Exercices corrigés
Calculs de fonctions dérivées
Exercices corrigés
Fonctions dérivées
Voir aussi: