Devoir de maths corrigé, Suites et fonction exponentielle
Première générale, spécialité mathématiques
Devoir de mathématiques, et corrigé, sur la fonction exeponentielle et les suites, arithmétiques et géométriques. Devoir posé en spé maths, première générale, année scolaire 2024/2025
Exercice 1: Variation d'une fonction avec exponentielle
Étudier le sens de variation de la fonction 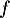 définie sur
définie sur 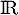 par
par
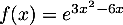 .
.
Préciser l'équation de la tangente au point d'abscisse 0.
On a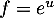 avec
avec 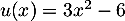 donc
donc 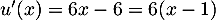 et donc
et donc
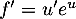 , soit
, soit
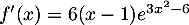
On peut alors dresser le tableau de variation:
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $-\infty$ && 1 && $+\infty$\\\hline
$6(x-1)$ && $-$ &\zb&$+$&\\\hline
$e^{3x^2-6}$ && $+$ &$|$ & $+$ &\\\hline
$f'(x)$ && $-$ &\zb&$+$&\\\hline
&&&&&\\
$f$&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&$e^{-3}$&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exvarpc2_c/6.png)
La tangente au point d'abscisse
au point d'abscisse 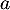 a pour équation réduite
a pour équation réduite
![\[T_a: y=f'(a)(x-a)+f(a)\]](/Generateur-Devoirs/1S/ChapExp/exvarpc2_c/9.png)
et donc, au point d'abscisse , on a l'équation
, on a l'équation
![\[T_0: y=f'(0)(x-0)+f(0)\]](/Generateur-Devoirs/1S/ChapExp/exvarpc2_c/11.png)
avec et
et 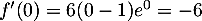 , on trouve l'équation
, on trouve l'équation
![\[T_0:y=-6x+1\]](/Generateur-Devoirs/1S/ChapExp/exvarpc2_c/14.png)
Cacher la correction
Préciser l'équation de la tangente au point d'abscisse 0.
Correction exercice 1
On a
On peut alors dresser le tableau de variation:
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $-\infty$ && 1 && $+\infty$\\\hline
$6(x-1)$ && $-$ &\zb&$+$&\\\hline
$e^{3x^2-6}$ && $+$ &$|$ & $+$ &\\\hline
$f'(x)$ && $-$ &\zb&$+$&\\\hline
&&&&&\\
$f$&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&$e^{-3}$&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exvarpc2_c/6.png)
La tangente
et donc, au point d'abscisse
avec
Cacher la correction
Exercice 2: Suite récurrente et suite intermédiaire arithmétique
On considère la suite numérique 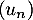 définie par
définie par 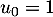 et, pour tout entier naturel
et, pour tout entier naturel 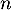 , par
, par 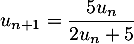 .
On définit aussi la suite
.
On définit aussi la suite 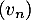 pour tout
pour tout 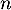 entier naturel par
entier naturel par
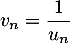 .
.
On considère la suite numérique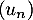 définie par
définie par 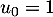 et, pour tout entier naturel
et, pour tout entier naturel 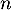 , par
, par 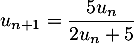 .
On définit aussi la suite
.
On définit aussi la suite 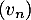 pour tout
pour tout 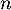 entier naturel par
entier naturel par
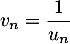 .
.
Cacher la correction
- Calculer
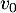 ,
, 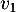 et
et 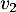 .
.
- Démontrer que
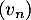 est une suite arithmétique, dont on donnera la raison.
est une suite arithmétique, dont on donnera la raison.
- En déduire l'expression de
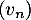 , puis celle de
, puis celle de
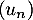 en fonction de
en fonction de 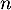 .
.
Correction exercice 2
On considère la suite numérique
-
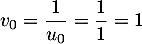 .
.
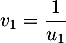 , avec
, avec
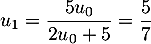 et donc
et donc 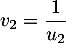
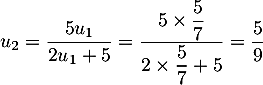 , avec
, avec
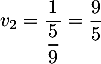 et donc
et donc 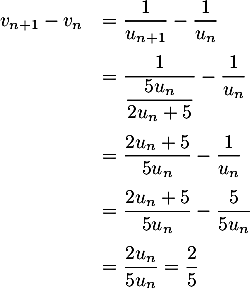
-
![\[\begin{array}{ll}
v_{n+1} - v_n
&= \dfrac1{u_{n+1}} - \dfrac1{u_n}\\[1.2em]
&= \dfrac1{\dfrac{5u_n}{2u_n+5}}-\dfrac1{u_n}\\[2.4em]
&=\dfrac{2u_n+5}{5u_n}-\dfrac1{u_n}\\[1.2em]
&=\dfrac{2u_n+5}{5u_n}-\dfrac5{5u_n}\\[1.2em]
&=\dfrac{2u_n}{5u_n}=\dfrac25\\
\enar\]](/Generateur-Devoirs/1S/Chap9/exinterar_c/15.png)
ainsi la suite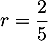 est arithmétique de raison
est arithmétique de raison
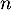 .
.
- On en déduit que, pour tout entier
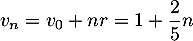 ,
,
 .
.
Ensuite, comme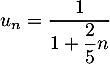 , on trouve finalement l'expression
, on trouve finalement l'expression
![\[u_n=\dfrac1{1+\dfrac25n}\]](/Generateur-Devoirs/1S/Chap9/exinterar_c/21.png)
Cacher la correction
Exercice 3: Problème complet: protocole médical, avec fonction exponentielle et suite récurrente (Bac 2022)
Dans le cadre d'un essai clinique on envisage deux protocoles de traiterment de
d'une maladie.
L'objectif de cet exercice est d'étudier, pour ces deux protocoles, l'évolution de la quantité de médicament présente dans le sang d'un patient en fonction du temps.
Les parties A et B sont indépendantes
Partie A : Étude du premier protocole
Le premier protocole consiste à faire absorber un médicament, sous forme de comprimé, au patient.
On modélise la quantité de médicament présente dans le sang du patient, exprimée en mg, par la fonction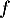 définie sur l'intervalle [0 ; 10] par
définie sur l'intervalle [0 ; 10] par
![\[f(t) = 3t e^{-0,5t+1},\]](/Generateur-Devoirs/1S/Chap9/bac2022/2.png)
où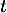 désigne le temps, exprimé en heure, écoulé depuis la prise du comprimé.
désigne le temps, exprimé en heure, écoulé depuis la prise du comprimé.
Partie B : Étude du deuxième protocole
Le deuxième protocole consiste à injecter initialement au patient, par piqüre intraveineuse, une dose de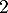 mg de médicament puis à réinjecter toutes les heures une dose de
mg de médicament puis à réinjecter toutes les heures une dose de 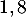 mg.
mg.
On suppose que le médicament se diffuse instantanément dans le sang et qu'il est ensuite progressivement éliminé.
On estime que lorsqu'une heure s'est écoulée après une injection, la quantité de médicament dans le sang a diminué de 30 % par rapport à la quantité présente immédiatement après cette injection.
On modélise cette situation à l'aide de la suite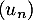 où, pour tout entier naturel
où, pour tout entier naturel 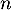 ,
, 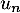 désigne la quantité de médicament, exprimée en mg, présente dans le sang du patient immédiatement après l'injection de la
désigne la quantité de médicament, exprimée en mg, présente dans le sang du patient immédiatement après l'injection de la 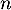 -ième heure. On a donc
-ième heure. On a donc 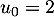 .
.
D'après Bac 2022, épreuve de spécialité
Partie A : Étude du premier protocole
Partie B : Étude du deuxième protocole
Cacher la correction
L'objectif de cet exercice est d'étudier, pour ces deux protocoles, l'évolution de la quantité de médicament présente dans le sang d'un patient en fonction du temps.
Les parties A et B sont indépendantes
Partie A : Étude du premier protocole
Le premier protocole consiste à faire absorber un médicament, sous forme de comprimé, au patient.
On modélise la quantité de médicament présente dans le sang du patient, exprimée en mg, par la fonction
où
-
Dresser le tableau de variation de
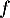 sur l'intervalle [0 ; 10].
sur l'intervalle [0 ; 10].
Selon cette modélisation, au bout de combien de temps la quantité de médicament présente dans le sang du patient sera-t-elle maximale ? Quelle est alors cette quantité maximale?
-
- Montrer que l'équation
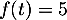 admet une unique solution sur l'intervalle [0 ; 2] notée
admet une unique solution sur l'intervalle [0 ; 2] notée 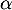 , dont on donnera une valeur approchée à
, dont on donnera une valeur approchée à 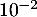 près.
On admet que l'équation
près.
On admet que l'équation 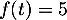 admet une unique solution sur l'intervalle [2 ; 10], notée
admet une unique solution sur l'intervalle [2 ; 10], notée 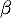 , et qu'une valeur approchée de
, et qu'une valeur approchée de 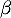 à
à 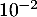 près est 3,46.
près est 3,46.
- On considère que ce traitement est efficace lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à 5 mg. Déterminer, à la minute près, la durée d'efficacité du médicament dans le cas de ce protocole.
- Montrer que l'équation
Partie B : Étude du deuxième protocole
Le deuxième protocole consiste à injecter initialement au patient, par piqüre intraveineuse, une dose de
On suppose que le médicament se diffuse instantanément dans le sang et qu'il est ensuite progressivement éliminé.
On estime que lorsqu'une heure s'est écoulée après une injection, la quantité de médicament dans le sang a diminué de 30 % par rapport à la quantité présente immédiatement après cette injection.
On modélise cette situation à l'aide de la suite
- Calculer, selon cette modélisation, la quantité
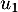 , de médicament (en mg) présente dans le sang du patient immédiatement après l'injection de la première heure.
, de médicament (en mg) présente dans le sang du patient immédiatement après l'injection de la première heure.
- Justifier que, pour tout entier naturel
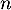 , on a :
, on a : 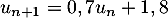 .
.
- On considère la suite
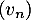 définie, pour tout entier naturel
définie, pour tout entier naturel 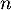 , par
, par 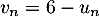 .
.
- Montrer que la suite
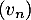 est une suite géométrique de raison
est une suite géométrique de raison 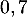 dont on précisera le premier terme.
dont on précisera le premier terme.
- Déterminer l'expression de
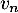 en fonction de
en fonction de 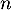 , puis de
, puis de 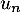 en fonction de
en fonction de 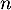 .
.
- Avec ce protocole, on arrête les injections lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à 5,5 mg. Déterminer, en détaillant les calculs, le nombre d'injections réalisées en appliquant ce protocole.
- Montrer que la suite
Correction exercice 3
D'après Bac 2022, épreuve de spécialité
Partie A : Étude du premier protocole
-
On a
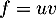 avec
avec 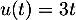 donc
donc 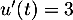 et
et 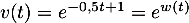 avec
avec
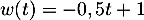 donc
donc 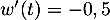 et alors
et alors 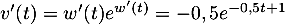 .
On obtient alors
.
On obtient alors 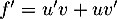 , soit
, soit
![\[\begin{array}{ll}f'(t)&=3e^{-0,5t+1}+3t\tm\lp-0,5e^{-0,5t+1}\rp\\[.4em]
&=3e^{-0,5t+1}\lp1-0,5t\rp\\[.4em]
&=3(-0,5t + 1)e^{-0,5t+1}\enar\]](/Generateur-Devoirs/1S/Chap9/bac2022_c/9.png)
On a alors le signe de lé dérivée et le sens de variation:
![\[\begin{tabular}{|c|*5c|}\hline
$t$ & 0 && 2 && 10 \\\hline
$-0,5t+1$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
$e^{-0,5t+1}$ && $+$ &\vline & $+$ & \\\hline
$f'(t)$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap9/bac2022_c/10.png)
Selon cette modélisation, la quantité maximale de médicament présente dans le sang du patient sera de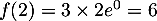 mg, au bout de 2 heures.
mg, au bout de 2 heures.
-
- Sur [0;2], la fonction
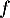 est continue (car même dérivable),
strictement croissante, avec
est continue (car même dérivable),
strictement croissante, avec 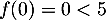 et
et 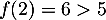 ,
et ainsi, d'après le théorème des valeurs intermédiaires
(théorème de la bijection), on sait donc qu'il existe une unique
solution
,
et ainsi, d'après le théorème des valeurs intermédiaires
(théorème de la bijection), on sait donc qu'il existe une unique
solution 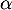 à l'équation
à l'équation 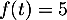 .
.
Avec la calculatrice, par balayage par exemple, on touve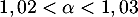 soit,
soit, 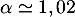 .
.
- On peut compléter le tableau de variation:
![\[\begin{tabular}{|c|*9c|}\hline
$t$ & 0 &&$\alpha$ && 2 &&$\beta$&& 10 \\\hline
&&&&&&&&&\\
$f$&&\psline[arrowsize=8pt]{->}(-.5,-.5)(1.3,.5)&5&&&
\psline[arrowsize=8pt]{->}(-.2,.5)(1.4,-.5)&5&&\\
&&&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap9/bac2022_c/19.png)
grâce auquel on trouve que la durée d'efficacité du médicament est donc de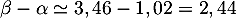 soit 2,44 heures, ou encore 2 heures et 26 minutes.
soit 2,44 heures, ou encore 2 heures et 26 minutes.
- Sur [0;2], la fonction
Partie B : Étude du deuxième protocole
- Selon cette modélisation, à la première heure la quantité dans le sang a diminué de 30%, il en reste donc
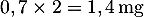 .
On réinjecte de plus une nouvelle dose de 1,8 mg, et on trouve donc que
.
On réinjecte de plus une nouvelle dose de 1,8 mg, et on trouve donc que
![\[u_1=0,7\tm2+1,8=3,2\]](/Generateur-Devoirs/1S/Chap9/bac2022_c/22.png)
- De même que précédemment, à la (n+1)-ème heure,
la quantité dans le sang présente l'heure précédente, soit
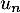 a diminué de 30%, soit
a diminué de 30%, soit 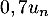 , et on réinjecte, donc ajoute, 1,8 mg.
, et on réinjecte, donc ajoute, 1,8 mg.
On obtient donc bien la relation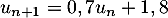 .
.
-
- Pour tout entier
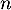 , on a
, on a
![\[\begin{array}{ll}v_{n+1}&=6-u_{n+1}\\
&=6-\lp0,7u_n+1,8\rp\\
&=4,2-0,7u_n\\
&=0,7\lp6-u_n\right)
=0,7v_n\enar\]](/Generateur-Devoirs/1S/Chap9/bac2022_c/27.png)
ce qui montre que la suite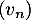 est bien géométrique de raison
est bien géométrique de raison 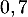 et de premier terme
et de premier terme 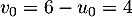 .
.
- On en déduit alors que, pour tout entier
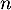 ,
,
![\[v_n=v_0\times q^n=4\times0,7^n\]](/Generateur-Devoirs/1S/Chap9/bac2022_c/32.png)
puis, comme , que
, que
![\[u_n=6-4\tm0,7^n\]](/Generateur-Devoirs/1S/Chap9/bac2022_c/34.png)
- On arrête les injections lorsque la quantité de médicament
présente dans le sang du patient est supérieure ou égale à 5,5 mg,
soit lorsque
![\[u_n\geqslant5,5\iff6-4\tm0,7^n\geqslant5,5\]](/Generateur-Devoirs/1S/Chap9/bac2022_c/35.png)
À l'aide de la calculatrice, on trouve que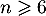 .
Comme on réalise une injection par heure, il faut donc en réaliser 6.
.
Comme on réalise une injection par heure, il faut donc en réaliser 6.
Remarque: en utilisant la fonction logarithme népérien, on trouve plus précisément que
![\[u_n\geqslant5,5\iff n\geqslant\dfrac{\ln(0,125)}{\ln(0,7)}\simeq5,8\]](/Generateur-Devoirs/1S/Chap9/bac2022_c/37.png)
- Pour tout entier
Cacher la correction
Quelques autres devoirs
Probabilités conditionnelles et calculs de probabilités avec un arbre de probabilités. Propriétés algébriques de l'exponentielle et une étude de fonctionDevoir: Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
étude de fonctions avec exponentielle, calculs de dérivées, et position relative d'une courbe et d'une droite
étude de fonctions avec exponentielle, premier devoir sur les suites: calcul des premiers termes et sens de variation, construction des premiers termes d'une suite
étude de fonctions avec exponentielle, variation et maximum. Suites numériques, étude de suites avec suites auxiliaires: arithmétiques et géométriques
dérivée et sens de variation d'une fonction rationnelle - Calculs algébriques et équations avec exponentielles - Probabilités conditionnelles et arbre de probabilité
Quelques exercices corrigés
Exercices corrigés
Construction des premiers termes d'une suite récurrente
Exercices corrigés
Suite récurrente, construction graphique des premiers termes
Exercices corrigés
Suite récurrente avec exponentielle, construction graphique des premiers termes
Exercices corrigés
Sens de variation d'une suite homographique
Exercices corrigés
Calcul des premieres termes et variation d'une suite récurrente
Voir aussi: