Devoir de maths corrigé, Produit scalaire et trigonométrie
Première générale, spécialité mathématiques
Devoir de mathématiques, et corrigé, sur le produit scalaire, trigonométrie et des équations de tangentes. Devoir posé en spé maths, première générale, année scolaire 2024/2025
Exercice 1: Produit scalaire: calcul d'un angle et de la distance à une droite
Dans le plan muni d'un repère orthonormé, soit les points
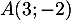 ,
, 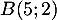 et
et 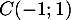 .
.
![\[\psset{unit=1cm,arrowsize=9pt}
\begin{pspicture}(-2.5,-3)(6,3)
\psline[linewidth=1.6pt]{->}(-2.3,0)(6,0)
\psline[linewidth=1.6pt]{->}(0,-3)(0,3)
\rput(3,-2){$\tm$}\rput(3.2,-2.2){$A$}
\rput(5,2){$\tm$}\rput(5.2,2.2){$B$}
\rput(-1,1){$\tm$}\rput[r](-1.2,1){$C$}
\pspolygon(3,-2)(5,2)(-1,1)
\multido{\i=-2+1}{8}{\psline(\i,-.1)(\i,.1)}
\multido{\i=-2+1}{5}{\psline(-.1,\i)(.1,\i)}
\psline(-1,1)(3.37,-1.25)\rput(3.6,-1.3){$H$}
\psline(3.2,-1.15)(3.3,-.94)(3.48,-1.03)
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap6/exangleproj_c/1.png)
Cacher la correction
- Calculer le produit scalaire
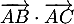
- Montrer que
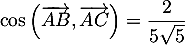 , puis en déduire l'angle
, puis en déduire l'angle 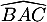 au dixième de degré près.
au dixième de degré près.
- Soit le point
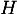 projection orthogonale du point
projection orthogonale du point 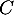 sur la droite
sur la droite 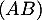 .
.
Calculer la longueur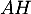 puis en déduire
puis en déduire 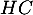 (donner les valeurs exactes).
(donner les valeurs exactes).
Correction exercice 1
![\[\psset{unit=1cm,arrowsize=9pt}
\begin{pspicture}(-2.5,-3)(6,3)
\psline[linewidth=1.6pt]{->}(-2.3,0)(6,0)
\psline[linewidth=1.6pt]{->}(0,-3)(0,3)
\rput(3,-2){$\tm$}\rput(3.2,-2.2){$A$}
\rput(5,2){$\tm$}\rput(5.2,2.2){$B$}
\rput(-1,1){$\tm$}\rput[r](-1.2,1){$C$}
\pspolygon(3,-2)(5,2)(-1,1)
\multido{\i=-2+1}{8}{\psline(\i,-.1)(\i,.1)}
\multido{\i=-2+1}{5}{\psline(-.1,\i)(.1,\i)}
\psline(-1,1)(3.37,-1.25)\rput(3.6,-1.3){$H$}
\psline(3.2,-1.15)(3.3,-.94)(3.48,-1.03)
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap6/exangleproj_c/1.png)
- On a
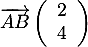 et
et 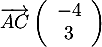 d'où
d'où 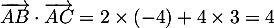
- On a aussi
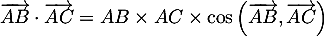 ,
avec
,
avec 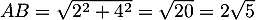 et
et 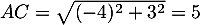 ,
,
d'où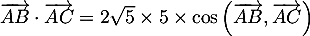 .
.
On a donc, en utilisant la question précédente,
![\[\overrightarrow{AB}\cdot\overrightarrow{AC}=4=2\sqrt5\tm5\tm\cos\lp\overrightarrow{AB},\overrightarrow{AC}\rp\]](/Generateur-Devoirs/1S/Chap6/exangleproj_c/9.png)
soit aussi
![\[\cos\lp\overrightarrow{AB},\overrightarrow{AC}\rp=\dfrac4{2\sqrt5\tm5}=\dfrac2{5\sqrt5}\]](/Generateur-Devoirs/1S/Chap6/exangleproj_c/10.png)
Avec l'aide de la caclulatrice, on trouve alors la valeur approché de l'angle
![\[\widehat{BAC}\simeq79,7^\circ\]](/Generateur-Devoirs/1S/Chap6/exangleproj_c/11.png)
- On peut soit utiliser la trigonométrie dans le triangle rectangle
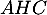 , dans lequel
, dans lequel
![\[\cos\hat{A}=\dfrac{AH}{AC}\]](/Generateur-Devoirs/1S/Chap6/exangleproj_c/13.png)
soit en utilisant les valeurs précédentes de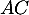 et du cosinus,
et du cosinus,
![\[\cos\hat{A}=\dfrac2{5\sqrt5}=\dfrac{AH}5\]](/Generateur-Devoirs/1S/Chap6/exangleproj_c/15.png)
d'où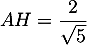
Deuxième méthode, avec le produit scalaire: comme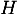 est le projeté orthogonal, on a
est le projeté orthogonal, on a
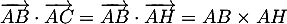 .
.
On en déduit alors, en tuilisant le théorème de Pythagore dans le triangle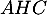 rectangle en
rectangle en 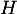 ,
,
![\[\begin{array}{lll}
&AC^2&=HC^2+AH^2\\\iff&HC^2&=AC^2-AH^2\\
&&=5^2-\lp\dfrac2{\sqrt5}\rp^2=\dfrac{121}5\enar\]](/Generateur-Devoirs/1S/Chap6/exangleproj_c/21.png)
d'où
![\[HC=\dfrac{11}{\sqrt5}\]](/Generateur-Devoirs/1S/Chap6/exangleproj_c/22.png)
Cacher la correction
Exercice 2: Inéquation sur le cercle trigonométrique
En s'aidant du cercle trigonométrique, résoudre dans ![$]-\pi;\pi[$](/Generateur-Devoirs/1S/Chap5/exineq/1.png) l'inéquation:
l'inéquation: 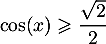 .
.
On connaît la valeur remarquable du cosinus: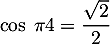 , et donc aussi par symétrie (et/ou formule trigonométrique)
, et donc aussi par symétrie (et/ou formule trigonométrique)
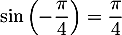 .
.
À l'aide du cercle trigonométrique, on trouve alors les solutions de l'inéquation:
![\[\cos(x)\geqslant\dfrac{\sqrt2}{2}
\iff x\in\lb-\dfrac\pi4;\dfrac\pi4\rb\]](/Generateur-Devoirs/1S/Chap5/exineq_c/3.png)
(.707,.707)
\rput(0.6,-.2){$\frac{\sqrt2}{2}$}
\psarc[linewidth=2pt,linecolor=blue](0,0){1}{-45}{45}
\psline(0,0)(1,-1)\rput(1.4,.5){$\dfrac\pi4$}
\psarc[arrowsize=7pt]{<-}(0,0){1.3}{-45}{-1}
\psline(0,0)(1,1)\rput(1.4,-.5){$-\dfrac\pi4$}
\psarc[arrowsize=7pt]{->}(0,0){1.3}{1}{45}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap5/exineq_c/4.png)
Cacher la correction
Correction exercice 2
On connaît la valeur remarquable du cosinus:
À l'aide du cercle trigonométrique, on trouve alors les solutions de l'inéquation:
(.707,.707)
\rput(0.6,-.2){$\frac{\sqrt2}{2}$}
\psarc[linewidth=2pt,linecolor=blue](0,0){1}{-45}{45}
\psline(0,0)(1,-1)\rput(1.4,.5){$\dfrac\pi4$}
\psarc[arrowsize=7pt]{<-}(0,0){1.3}{-45}{-1}
\psline(0,0)(1,1)\rput(1.4,-.5){$-\dfrac\pi4$}
\psarc[arrowsize=7pt]{->}(0,0){1.3}{1}{45}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap5/exineq_c/4.png)
Cacher la correction
Exercice 3: Tangentes perpendiculaires à une parabole
Soit 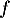 la fonction définie sur
la fonction définie sur 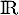 par l'expression
par l'expression
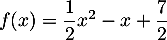 et
et 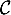 sa courbe représentative
dans un repère orthonormal du plan.
sa courbe représentative
dans un repère orthonormal du plan.
On note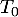 la tangente à
la tangente à 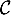 au point d'abscisse 0 et
au point d'abscisse 0 et 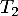 la tangente à
la tangente à 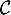 au point d'abscisse 2.
au point d'abscisse 2.
Cacher la correction
On note
- Donner l'équation de
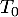 .
.
- Déterminer les coordonnées du point
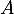 d'intersection de
d'intersection de 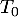 avec l'axe des abscisses, puis du point
avec l'axe des abscisses, puis du point 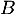 d'intersection de
d'intersection de 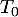 avec l'axe des ordonnées.
avec l'axe des ordonnées.
- Donner l'équation de
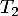 .
.
- Montrer que les droites
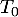 et
et 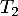 sont perpendiculaires.
sont perpendiculaires.
Correction exercice 3
- On a
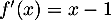 et donc, la tangente
et donc, la tangente 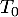 à
à 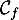 en 0 a pour équation
en 0 a pour équation 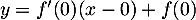 ,
avec
,
avec 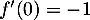 et
et 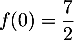 , d'où l'équation
, d'où l'équation
![\[T_0: y=-x+\dfrac72\]](/Generateur-Devoirs/1S/Chap6/extgtP_c/7.png)
- On a
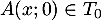 et donc
et donc 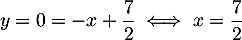 , et donc
, et donc
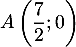
De même, on a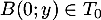 et donc
et donc 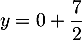 , et donc
, et donc
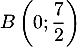
- La tangente
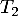 à
à 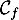 en 2 a pour équation
en 2 a pour équation
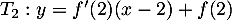 soit,
avec
soit,
avec 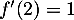 et
et 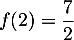 , l'équation
, l'équation
![\[T_2: y=1(x-2)+\dfrac72=x+\dfrac32\]](/Generateur-Devoirs/1S/Chap6/extgtP_c/19.png)
- On peut suivre l'idée de la question b) et chercher aussi les points d'intersection de
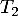 avec les axes du repère.
avec les axes du repère.
On trouve les points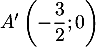 et
et 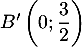 .
.
Maintenant, les droites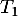 et
et 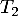 sont perpendiculaires si et seulement si les vecteurs
sont perpendiculaires si et seulement si les vecteurs 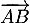 et
et 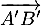 sont orthogonaux, et donc si et seulement si
sont orthogonaux, et donc si et seulement si
![\[\overrightarrow{AB}\cdot\overrightarrow{A'B'}=0\]](/Generateur-Devoirs/1S/Chap6/extgtP_c/27.png)
Or,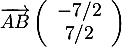 et
et 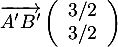 , d'où
, d'où
![\[\overrightarrow{AB}\cdot\overrightarrow{A'B'}=\lp-\dfrac72\rp\tm\dfrac32+\dfrac72\tm\dfrac32=0\]](/Generateur-Devoirs/1S/Chap6/extgtP_c/30.png)
ce qui montre que ces vecteurs sont bin orthongonaux, et donc les droites bien perpendiculaires.
Cacher la correction
Quelques autres devoirs
dérivées et étude de fonction. Angles en radians sur le cercle trigonométrique et en mesure principale
Géométrie avec le produit scalaire, projeté orthogonal et calcul d'un angle et droites tangentes à une parabole perpendiculaires
Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
Probabilités conditionnelles et calculs de probabilités avec un arbre de probabilités. Propriétés algébriques de l'exponentielle et une étude de fonctionDevoir: Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
Mesure principale d'un angle en radians - Etude des variations d'une fonctions - Etude d'une fonction auxilaire et TVI
Quelques exercices corrigés
Exercices corrigés
Droites perpendiculaires ou parallèles
Exercices corrigés
Calcul d'un angle et distance d'un point à une droite: projeté orthogonal
Exercices corrigés
Valeur approchée d'un angle avec le produit scalaire
Exercices corrigés
Calculs vectoriels et produit scalaire
Exercices corrigés
Projeté orthogonal sur une droite et calcul d'un angle
Voir aussi: