Conduite accompagnée et réussite au permis de conduire

Exercice corrigé - Spécialité maths, première générale

Énoncé

Pour préparer l'examen du permis de conduire, on distingue deux types de formation :
  • la formation avec conduite accompagnée ;
  • la formation traditionnelle.

On considère un groupe de 300 personnes venant de réussir l’examen du permis de conduire. Dans ce groupe :
  • 75 personnes ont suivi une formation avec conduite accompagnée ; parmi elles, 50 ont réussi l’examen à leur première présentation et les autres ont réussi à leur deuxième présentation.
  • 225 personnes se sont présentées à l’examen suite à une formation traditionnelle ; parmi elles, 100 ont réussi l’examen à la première présentation, 75 à la deuxième et 50 à la troisième présentation.


On interroge au hasard une personne du groupe considéré, et on considère les évènements suivants :
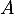  • $A$ : « la personne a suivi une formation avec conduite accompagnée » ;
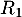  • $R_1$ : « la personne a réussi l’examen à la première présentation » ;
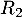  • $R_2$ : « la personne a réussi l’examen à la deuxième présentation » ;
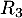  • $R_3$ : « la personne a réussi l’examen à la troisième présentation ».

  1. Modéliser la situation par un arbre pondéré.
  2. Calculer la probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l’examen à sa deuxième présentation.
  3. Quelle est la probabilité que la personne interrogée ait réussi l’examen à sa deuxième présentation.
  4. La personne interrogée a réussi l’examen à sa deuxième présentation. Quelle est la probabilité qu’elle ait suivi une formation avec conduite accompagnée?



Correction

Correction

  1. On modélise la situation par un arbre pondéré.
    \[\begin{pspicture}(0,-2.6)(5,2.6) \psline(2,-1.5)(0,0)(2,1.5) \rput(.8,1.1){$\frac{75}{300}$}\rput(2.2,1.5){$A$} \rput(.8,-1.1){$\frac{225}{300}$}\rput(2.2,-1.5){$\overline{A}$} % \psline(2.5,1.5)(4,1.5) \psline(4,.5)(2.5,1.5)(4,2.5) \rput(4.3,2.5){$R_1$}\rput(3.3,2.4){$\frac{50}{75}$} \rput(4.3,1.5){$R_2$}\pscircle[linestyle=none,fillstyle=solid,fillcolor=white](3.3,1.6){.3}\rput(3.3,1.6){$\frac{25}{75}$} \rput(4.3,.5){$R_3$}\rput(3.3,.7){$0$} % \psline(2.5,-1.5)(4,-1.5) \psline(4,-.5)(2.5,-1.5)(4,-2.5) \rput(4.3,-.5){$R_1$}\rput(3.3,-.5){$\frac{100}{225}$} \rput(4.3,-1.5){$R_2$}\pscircle[linestyle=none,fillstyle=solid,fillcolor=white](3.3,-1.6){.3}\rput(3.3,-1.5){$\frac{75}{225}$} \rput(4.3,-2.5){$R_3$}\rput(3.3,-2.4){$\frac{50}{225}$} \end{pspicture}\]


  2. La probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l'examen à sa deuxième présentation est:
    \[\begin{array}{ll}P\left( A\cap R_2\rp&= P(A)\times P_{A}\left( R_2\rp\\[.3em] &=\dfrac{75}{300}\tm\dfrac{25}{75}=\dfrac{1}{12}\enar\]

  3. La probabilité que la personne interrogée ait réussi l'examen à sa deuxième présentation est 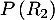$P\left( R_2\rp$ soit, d'après la formule des probabilités totales,
    \[\begin{array}{ll} P\left( R_2\right) %&= P\left( A\cap R_2\right) + P\left(\overline{A}\cap R_2\right)\\ &=P(A\cap R_2)+P(\overline{A}\cap R_2)\\[.5em] &=\dfrac{75}{300}\tm\dfrac{25}{75} +\dfrac{225}{300}\tm\dfrac{75}{225}\\[1em] &=\dfrac{25}{300} + \dfrac{75}{300} =\dfrac{100}{300}=\dfrac13\enar\]

  4. La personne interrogée a réussi l'examen à sa deuxième présentation. La probabilité qu'elle ait suivi une formation avec conduite accompagnée est alors la probabilité conditionnelle:
    \[P_{R_2}(A) = \dfrac{P(A\cap R_2)}{P(R_2)}= \dfrac{\dfrac1{12}}{\dfrac13} = \dfrac3{12}=\dfrac14 \]



Tag:Probabilités conditionnelles

Autres sujets au hasard: Lancer de dés


Voir aussi:

Quelques devoirs