Méthodes numériques
Y. Morel
- Résolution d'équations
- Calcul numérique d'intégrales
- Méthode des rectangles (à gauche et droite)
- Méthode des rectangles (point milieu)
- Méthode des trapèzes
- Méthode de Simpson
- Généralités sur les méthodes d'intégration numrique
- Méthodes de Gauss
- Résolution numérique d'équations différentielles (EDO)
Résolution d'une équation de la forme
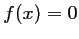
Résolution par dichotomie
La récherche d'une solution approchée à l'équation
Ce nouvel intervalle est alors redécoupé en deux...et ainsi de
suite jusqu'à ce que la longueur de l'intervalle dans lequel on
recherche la solution soit inférieure à la précision
![]() souhaitée.
souhaitée.
![$\displaystyle \fbox{\begin{minipage}[t]{6cm}
Initialisation de $a$, $b$\ et $\...
...
\hspace*{\ProgIndent} Fin Si \\
Fin Tant que \\
Afficher $x$
\end{minipage}}$](/MathAppli/Methodes-Numeriques/img4.png)
Méthode de Newton
C'est une méthode de descente, c'est-à-dire que l'approximation trouvée à chaque itération est meilleure que celle trouvée à l'étape précédente.
En partant d'une valeur
![]() , on "descend" donc pour la méthode de
Newton le long de la tangente (dont le coefficient directeur est la
dérivée de
, on "descend" donc pour la méthode de
Newton le long de la tangente (dont le coefficient directeur est la
dérivée de
![]() en
en
![]() :
:
![]() ) à la courbe représentative de
) à la courbe représentative de
![]() jusqu'à l'axe des abscisses.
On utilise alors l'abscisse de ce point comme nouvelle valeur pour
jusqu'à l'axe des abscisses.
On utilise alors l'abscisse de ce point comme nouvelle valeur pour
![]() , jusqu'à atteindre la précision
, jusqu'à atteindre la précision
![]() souhaitée.
souhaitée.
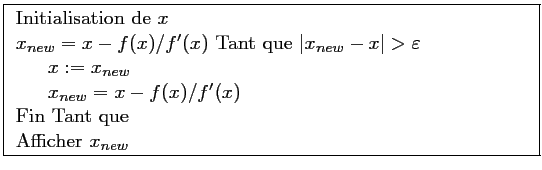
Méthode de la sécante
Comme on peut ne pas connaître explicitement la fonctionDans la méthode de la sécante, on approxime la tangente à la courbe de
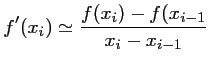 .
.
L' algorithme devient:

Calcul numérique d'intégrales
On cherche à calculer l'intégrale
 .
.
On discrétise l'intervalle
On a alors,
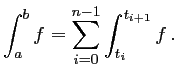
A l'aide d'un changement de variable, on ramène les
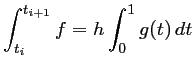 avec
avec
Il reste à calculer cette intégrale.
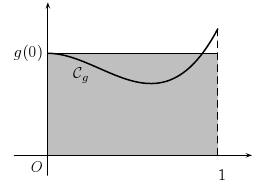
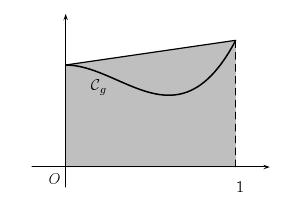
Méthode des rectangles
On approxime "grossièrement" l'aire sous la courbe de la fonction par l'aire d'un rectangle.
Rectangle à gauche:
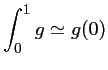
|
Rectangle à droite:
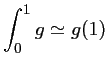
|
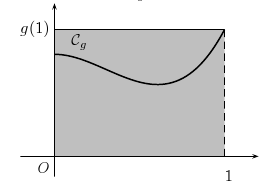
Méthode du point milieu
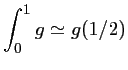
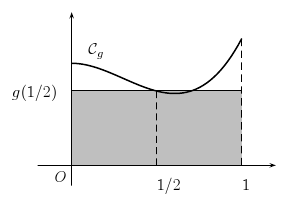
Méthode des trapèzes
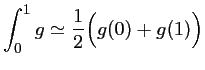
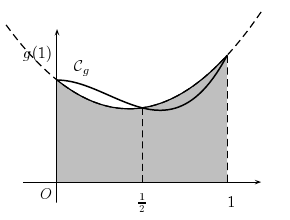
Méthode de Simpson
On interpole la fonction
On approxime alors l'intégrale de
![\begin{array}{ll}
\displaystyle \int_0^1 g &\displaystyle \si...
...space{0.2cm}\\
&=\dfrac{1}{6}\left[2a+3b+6c\right]
\end{array}](/MathAppli/Methodes-Numeriques/img38.png)
|
|
Il reste à déterminer les coefficients

En remplaçant ces valeurs dans l'expression de l'intégrale, on obtient:
![$\int_0^1 g \simeq \dfrac{1}{6}\left[2a+3b+c\right]
=\dfrac{1}{6}\left[g(1)+4g\left(\frac{1}{2}\right)+g(0)\right]
$](/MathAppli/Methodes-Numeriques/img44.png)
Plus généralement:
Toutes les méthodes précédentes consistent à interpoler la fonction par un polynôme, puis à remplacer le calcul de l'intégrale de celle-ci par l'intégrale du polynôme d'interpolation.Pour les méthodes des rectangles, on interpole la fonction en un seul point avec un polynôme constant (à gauche, milieu ou droite de l'intervalle); la méthode des trapèzes utilise l'interpolation de la fontion par un polynôme du premier degré (
On peut construire ainsi des méthodes d'intégration numérique d'ordre quelconque, en augmentant le degré du polynôme d'interpolation. Il s'agit plus généralement des méthodes de Newton-Cotes.
Méthode de Gauss
Les méthodes numériques précédentes utilisent toutes une discrétisation régulière de l'intervalle d'intégration. On peut penser, au lieu de découper cet intervalle régulièrement, à choisir des points de manière plus adaptée.C'est ce à quoi aboutissent les méthodes de Gauss pour l'intégration numérique ...
Résolution numérique d'EDO
On considère l'équation différentielle ordinaire (EDO) du premier ordre
EDO et intégration numérique
Après discrétisation de l'intervalle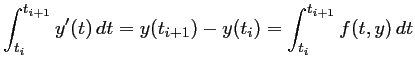
soit,

Définir un schéma d'intégration numérique pour une EDO revient alors à utiliser une méthode d'intégration numérique (rectangle, trapèzes, Simpson, ...).
Méthodes d'Euler (
 1770)
1770)
La méthode des rectangles à gauche fournit la méthode d'Euler:

On peut utiliser aussi la méthode des rectangles à droite. On aboutit alors au schéma d'Euler implicite, ou rétrograde:
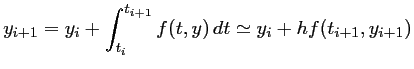
C'est un schéma implicite (expression de l'inconnue
On résout cette équation, dont la seule inconnue est
Ce schéma est donc un peu plus compliqué, et un peu plus lourd à mettre en
Avec la même idée, on peut penser à utiliser une intégration numpérique par la méthode des trapèzes. La méthode d'Euler obtenue est souvent alors appelée méthode d'Euler modifiée:
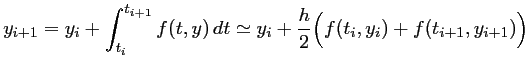
Formule de Taylor et différences finies
Les méthodes de différences finies reposent sur la formule de taylor: au voisinage de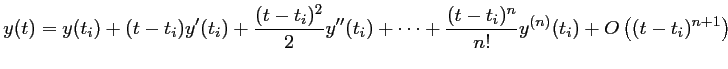
d'où, en
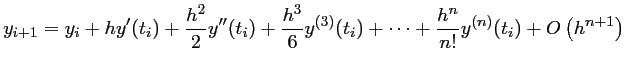
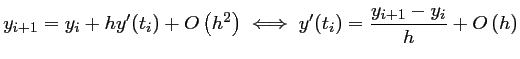 , d'où l'approximation
, d'où l'approximation
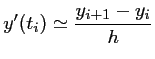 qui est utilisé par la méthode d'Euler.
C'est une approximation de la dérivée d'ordre
qui est utilisé par la méthode d'Euler.
C'est une approximation de la dérivée d'ordre
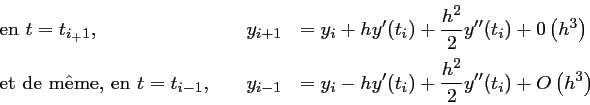
soit, en soustrayant ces deux relations:
d'où,
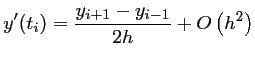
C'est un schéma centré, fournissant une approximation de la dérivée d'ordre 2.
on peut aussi par exemple, et pour plus de précision, prendre en compte les points

soit,
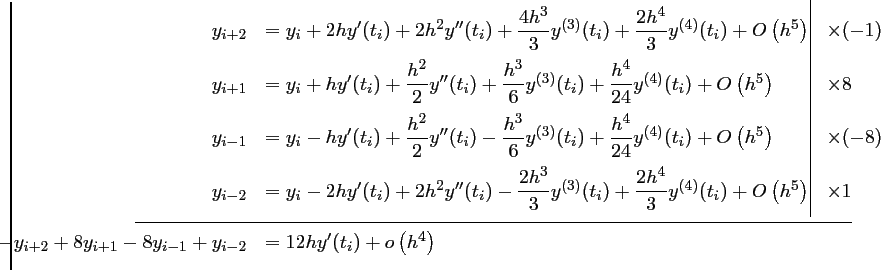
d'où,
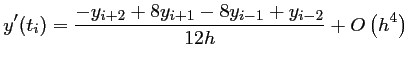
C'est un schéma centré, fournissant une approximation de la dérivée
On peut aussi, au lieu d'utiliser les valeurs
La méthode des différences finies permet de discrétiser la plupart des équations différentielles ordinaires et des équations aux dérivées partielles de la physique assez simplement.
Différences finies et méthode d'Euler (1768)
Approximation de la dérivée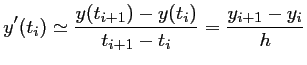
d'où la relation de récurrence:

Il s'agit donc d'une méthode d'ordre
Méthodes de Runge Kutta (RK) (
 )
)
Les méthodes de Runge et Kutta repose fondamentalement sur la formule de Taylor. L'idée de Runge et Kutta est d'écrire une solution approchée
- Runge-Kutta 1 (RK1):
La formule de Taylor à l'ordre 1 s'écrit
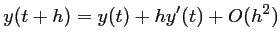
Soit, en utilsant l'équation différentielle: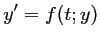 ,
,

Elle coïncide donc avec la méthode d'Euler.
- Runge-Kutta 2 (RK2):
La formule de Taylor à l'ordre 2 s'écrit:
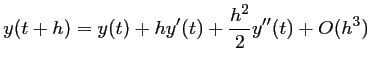
dans laquelle on peut détailler à l'aide de l'équation différentielle:
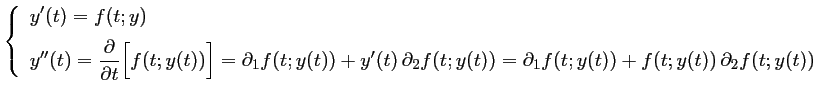
On substitue alors ces deux expressions dans le développement de Taylor:
![$y(t+h)=y(t)+hf(t;y)+
\dfrac{h^2}{2}\Bigl[
\partial_1 f(t;y)+f(t;y)\,\partial_2 f(t;y)
\Bigr]+O(h^3)$](/MathAppli/Methodes-Numeriques/img89.png)
L'idée de Runge et Kutta est d'introduire une combinaison linéaire dans le calcul de entre
entre
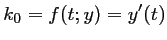 , la dérivée en
, la dérivée en
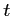 , et
, et
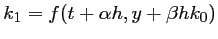 , la dérivée un "peu plus loin":
, la dérivée un "peu plus loin":
![$y(t+h)=y(t)+h\Bigl[ Ak_0+Bk_1\Bigr]$](/MathAppli/Methodes-Numeriques/img94.png)
Ensuite, en appliquant le développement de Taylor de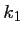 , puis comparant à celui de
, puis comparant à celui de
 précédent,
on espère obtenir des valeurs pour les coefficients
précédent,
on espère obtenir des valeurs pour les coefficients
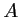 ,
,
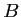 ,
,
 et
et
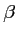 .
Ce développement s'écrit:
.
Ce développement s'écrit:

En reportant ces expressions de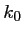 et
et
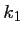 dans la combinaison linéaire souhaitée de
dans la combinaison linéaire souhaitée de
 , on obtient:
, on obtient:
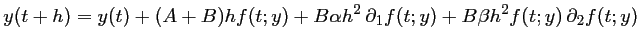
puis, en identifiant avec la série de Taylor à l'ordre 2, on trouve que les coefficients doivent vérifier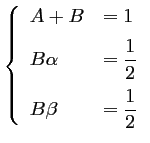
Ainsi, lorsque les paramètres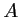 ,
,
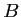 ,
,
 et
et
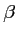 vérifient ces relations, la combinaison linéaire proposée aura la
même ordre d'approximation que la série de Taylor,
c'est-à-dire un ordre 2.
vérifient ces relations, la combinaison linéaire proposée aura la
même ordre d'approximation que la série de Taylor,
c'est-à-dire un ordre 2.
Ce système est surdéterminé: seulement 3 équations pour 4 inconnues, et admet donc une infinité de solutions.
On peut fixer par exemple arbitrairement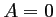 , et alors,
, et alors,
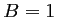 ,
,
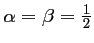 , et le schéma correspondant s'écrit:
, et le schéma correspondant s'écrit:
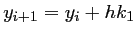 avec,
avec,
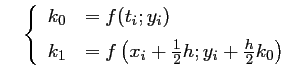
- Runge-Kutta 4 (RK4):
L'idée de la méthode reste la même que
précédemment.
On écrit
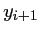 comme une combinaison linéaire:
comme une combinaison linéaire:

avec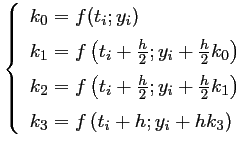
En utilisant le développement de Taylor à l'ordre 4:

et en identifiant les coefficients, après écrit les développements de Taylor au même ordre de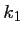 ,
,
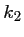 et
et
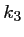 ,
on trouve
,
on trouve
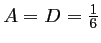 , et
, et
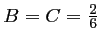 , d'où le schéma RK4:
, d'où le schéma RK4:
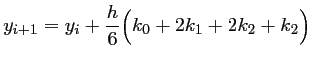
avec les valeurs de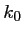 ,
,
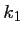 ,
,
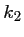 et
et
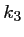 précédentes.
précédentes.
Voir aussi