Organisation d'un concert de musique

Exercice corrigé - Spécialité maths, première générale

Énoncé

Un groupe d'élèves d'une classe de première générale veut organiser un concert de musique à l'intérieur du lycée. Il fait une enquête pour connaître le nombre d'élèves souhaitant assister à ce concert.
450 élèves ont répondu à cette enquête, 180 garçons et 270 filles. 144 filles et 72 garçons sont favorables et souhaitent assister au concert.
Par la suite, on note les événements:
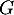$G$: « l'élève est un garçon»
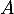$A$: « l'élève souhaite assister au concert»
  1. On prend la fiche au hasard d'un élève ayant répondu à cette enquête.
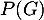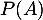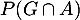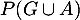    Donner les probabilités $P(G)$, $P(A)$, $P(G\cap A)$ et $P(G\cup A)$.
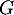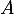  2. Les événements $G$ et $A$ sont-ils indépendants ?
  3. Calculer la probabilité 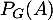$P_G(A)$, et interpréter cette probabilité (avec une phrase).
  4. Au concert, un élève devant moi me dérange. Quelle est la probabilité que ce soit un garçon ?



Correction

Correction

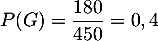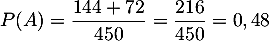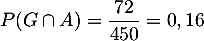  1. On a $P(G)=\dfrac{180}{450}=0,4$, $P(A)=\dfrac{144+72}{450}=\dfrac{216}{450}=0,48$, $P(G\cap A)=\dfrac{72}{450}=0,16$ et donc
    \[P(G\cup A)=P(G)+P(A)-P(G\cap A)=0,72\]


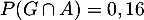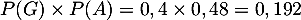  2. On a $P(G\cap A)=0,16$ et $P(G)\times P(A)=0,4\times0,48=0,192$, donc ces événements ne sont pas indépendants.
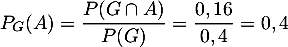  3. $P_G(A)=\dfrac{P(G\cap A)}{P(G)}=\dfrac{0,16}{0,4}=0,4$.
    Ainsi, sachant qu'on parle d'un garçon, la probabilité qu'il souhaite assister au concert est de 40%.
  4. On cherche la probabilité conditionnelle
    \[P_A(G)=\dfrac{P(A\cap G)}{P(A)}=\dfrac{0,16}{0,48}\simeq0,33\]



Tag:Probabilités conditionnelles

Autres sujets au hasard: Lancer de dés


Voir aussi:

Quelques devoirs