Jeunes et transports en commun

Exercice corrigé - Spécialité maths, première générale

Énoncé

Dans tout cet exercice, les probabilités seront arrondies, si nécessaire, à 10−3.
D'après une étude, les utilisateurs réguliers de transports en commun représentent 17 % de la population française. Parmi ces utilisateurs réguliers, 32 % sont des jeunes âgés de 18 à 24 ans. (Source : TNS-Sofres)


On interroge une personne au hasard et on note les événements:
  • R: « La personne interrogée utilise régulièrement les transports en commun ».
  • J: « La personne interrogée est âgée de 18 à 24 ans ».

  1. Représentez la situation à l'aide d'un arbre pondéré.
  2. Quelle est la probabilité que la personne interrogée soit un jeune de moins de 24 ans utilisateur régulier des transports en commun.
  3. D'après cette même étude, les jeunes de 18 à 24 ans représentent 11 % de la population française.
    Calculer alors la proportion de jeunes de 18 à 24 ans parmi les utilisateurs non réguliers des transports en commun.
  4. Je discute avec un jeune étudiant, de moins de 24 ans, que je ne connaît pas. Quelle est la probabilité qu'il soit un utilisateur régulier des transport en communs.



Correction

Correction

(d'après Bac centres étrangers, 9 juin 2021)

  1. \[\psset{xunit=1.3cm,yunit=.8cm} \begin{pspicture}(-.4,-2)(4.2,2) \psline(0,0)(1.5,1)\rput(1.75,1){$R$} \rput(.8,.9){17\%} \rput(.8,-.9){83\%} \psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{R}$} \psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$J$} \rput(2.8,1.7){32\%} \rput(2.8,.3){68\%} \psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{J}$} \psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{J}$} \psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$J$} \end{pspicture}\]


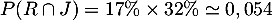
  2. On cherche ici la probabilité de l'intersection: $P(R\cap J)=17\%\tm32\%\simeq0,054$
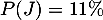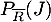  3. On sait donc de plus que $P(J)=11\%$, et on cherche la probabilité que la personne soit un jeune parmi les utilisateurs non réguliers, c'est-à-dire la probabilité $P_{\overline{R}}(J)$.
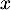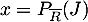    On note donc $x$ cette probabilité conditionnelle: $x=P_{\overline{R}}(J)$,
    \[\psset{xunit=1.3cm,yunit=.8cm} \begin{pspicture}(-.4,-2)(4.2,2) \psline(0,0)(1.5,1)\rput(1.75,1){$R$} \rput(.8,.9){17\%} \rput(.8,-.9){83\%} \psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{R}$} \psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$J$} \rput(2.8,1.7){32\%} \rput(2.8,.3){68\%} \psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{J}$} \psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{J}$} \rput(2.8,-.35){$x$} \rput(2.8,-1.7){$1-x$} \psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$J$} \end{pspicture}\]

    On a alors d'après la formule des probabilités totales,
    \[\begin{array}{ll} P(J)&=P(J\cap R)+P(J\cap\overline{R})\\[.3em] &=17\%\tm32\%+83\%\tm x \enar\]

    d'où
    \[\begin{array}{ll}&83\%x+17\%\tm32\%=11\%\\ \iff& x=\dfrac{11\%-17\%\tm32\%}{83\%}\simeq 6,7\% \enar\]

    Ainsi, parmi les utilisateurs non réguliers, environ 6,7% sont des jeunes de moins de 24 ans.
  4. On cherche cette fois la probabilité conditionnelle
    \[P_{J}(R) =\dfrac{P\left( J\cap R\right)}{P\left( J\right)} \simeq\dfrac{17\%\tm32\%}{11\%}\simeq49,4\%\]

    soit environ une chance sur deux.


Tag:Probabilités conditionnelles

Autres sujets au hasard: Lancer de dés


Voir aussi:

Quelques devoirs