Des créatures riches et généreuses

Exercice corrigé - Spécialité maths, première générale

Énoncé

Sur la planète Mercurne, 99% des créatures sont riches ou généreuses et il y a autant de créatures riches que de créatures généreuses. De plus, chez les créatures de cette planète, les caractères "riches" et "généreux" sont indépendants et non apparents. On rencontre une créature de cette planète et on note respectivement R et G les événements "cette créature est riche" et "cette créature est généreuse". On pose 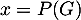$x = P (G)$.
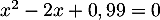  1. Montrer que x vérifie: $x^2 - 2x + 0, 99 = 0$.
  2. Quelle est la probabilité que cette créature soit riche et généreuse ?



Correction

Correction

  1. On a, d'après l'énoncé,
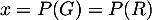
    • $x=P(G)=P(R)$
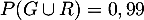
    • $P(G\cup R)=0,99$
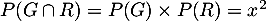    • $P(G\cap R)=P(G)\times P(R)=x^2$, par indépendance de ces événements
    On a aussi, reliant les probabilités de la réunion et de l'intersection,
    \[P(G\cup R)=P(G)+P(R)-P(G\cap R)\]

    soit encore
    \[0,99 = x + x - x^2 \iff x^2-2x+0,99=0\]


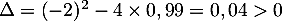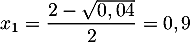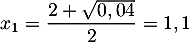  2. On résout alors cette équation du second degré, qui a pour discriminant $\Delta=(-2)^2-4\tm0,99=0,04>0$ et qui admet donc deux racines réelles distinctes $x_1=\dfrac{2-\sqrt{0,04}}2=0,9$ et $x_1=\dfrac{2+\sqrt{0,04}}2=1,1$.
    La deuxième solution est impossible ici, car pour une probabilité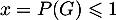 $x=P(G)\leqslant1$, donc nécessairement $x=0,9$.
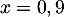    La probabilité que la créature rencontrée au hasard soit riche et généreuse à la fois est donc
    \[P(G\cap R)=x^2=0,81\]



Tag:Probabilités conditionnelles

Autres sujets au hasard: Lancer de dés


Voir aussi:

Quelques devoirs