Equations et inéquations avec des exponentielles

Exercice corrigé - Spécialité maths, première générale

Énoncé

Résoudre les équations et inéquations:
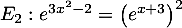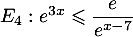
$E_1: e^{x+2}=1$  ,   $E_2: e^{3x^2-2}=\left( e^{x+3}\rp^2$  ,   $E_3: e^3e^x<1$  et $E_4: e^{3x}\leqslant\dfrac{e}{e^{x-7}}$


Correction

Correction

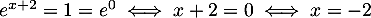  1. $e^{x+2}=1=e^0\iff x+2=0 \iff x=-2$, donc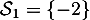 $\mathcal{S}_1=\la-2\ra$
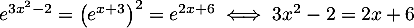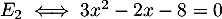  2. $e^{3x^2-2}=\left( e^{x+3}\rp^2=e^{2x+6}\iff 3x^2-2=2x+6$, car la fonction exponentielle est strictement croissante, et donc $E_2\iff 3x^2-2x-8=0$.
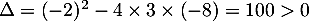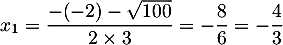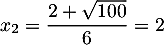    Cette équation du second degré a pour dsicriminant $\Delta=(-2)^2-4\tm3\tm(-8)=100>0$ et admet donc deux solutions réelles $x_1=\dfrac{-(-2)-\sqrt{100}}{2\tm3}=-\dfrac86=-\dfrac43$ et $x_2=\dfrac{2+\sqrt{100}}6=2$.
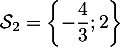
    Ainsi, $\mathcal{S}_2=\la-\dfrac43 ; 2\ra$
  3. $e^3e^x=e^{3+x}<1=e^0\iff 3+x<0$ car la fonction exponentielle est strictement croissante, et donc $E_3\iff x<-3$, soit les solutions $\mathcal{S}_3=]-\infty ; -3[$
  4. En multipliant par 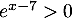$e^{x-7}>0$, donc l'ordre ne change pas, on obtient
    \[E_4 \iff e^{3x}e^{x-7}=e^{4x-7}\leqslant e=e^1\]

    et, comme la fonction exponentielle est strictement croissante,
    \[E_4\iff 4x-7\leqslant 1\iff x\leqslant2\]

    soit donc les solutions $\mathcal{S}_4=]-\infty ; 2]$


Tag:Exponentielle

Autres sujets au hasard: Lancer de dés


Voir aussi:

Quelques devoirs