Distance parcourue par une balle rebondissante

Exercice corrigé - Spécialité maths, première générale

Énoncé

On lâche une balle de 2m de hauteur. Cette balle rebondit à chaque fois à une hauteur égale aux trois quarts de la hauteur à laquelle elle a été lâchée.
  1. Calculer la hauteur du 1er rebond, puis la hauteur du 2ème rebond.
  2. On arrête cette balle au sommet du 20ème rebond.
    Quelle est la hauteur de ce 20ème rebond ? Quelle distance totale aura alors parcouru cette balle pendant ces 20 rebonds ?



Correction

Correction

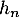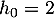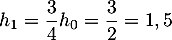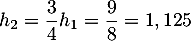
  1. On note $h_n$ la hauteur, en mètres, du n-ième rebond. On a $h_0=2$, et la hauteur du 1er rebond $h_1=\dfrac34h_0=\dfrac32=1,5$, puis celle du 2ème rebond $h_2=\dfrac34h_1=\dfrac98=1,125$
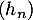  2. La suite $(h_n)$ est géométrique de raison 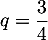$q=\dfrac34$, et alors, au 20ème rebond, on a
    \[h_{20}=h_0q^{20}=2\tm\lp\dfrac34\rp^{20}\simeq0,006\]

    soit une hauteur d'environ 0,6cm.

    En l'arrêtant au sommet du 20ème rebond, la balle aura parcouru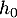 $h_0$, puis deux fois 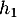$h_1$ (monté puis descente) puis deux fois 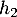$h_2$, …, jusqu'à une fois 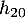$h_{20}$ (on l'arrête cette fois au sommet, et elle ne redescend donc pas). La distance totale parcourue est donc
    \[d=h_0+2h_1+2h_2+\dots+2h_{19}+h_{20}\]

    soit
    \[d=2\bigl(h_0+h_1+\dots+h_{20}\bigr) -h_0-h_{20}\]

    La première somme vaut
    \[\begin{array}{ll}h_0+\dots+h_{20}&=h_0\lp1+q+\dots+q^{20}\rp\\[.5em] &=h_0\dfrac{1-q^{21}}{1-q}\\ &=2\dfrac{1-\lp\dfrac34\rp^{21}}{1-\dfrac34}\\ &=8\lp1-\lp\dfrac34\rp^{21}\rp\enar\]

    et la distance totale parcourue est alors
    \[\begin{array}{ll}d&=2\tm8\lp1-\lp\dfrac34\rp^{21}\rp-2-2\lp\dfrac34\rp^{20}\\ &\simeq13,96\enar\]

    soit un peu moins de 14 mètres parcourus.


Tag:Suites

Autres sujets au hasard: Lancer de dés


Voir aussi:
LongPage: h2: 3 - h3: 0