Suite définie par récurrence et suite intermédiaire géométrique
Exercice corrigé - Spécialité maths, première générale
Énoncé
Soit la suite 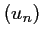 définie par
définie par
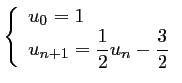 .
.
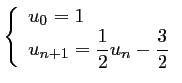 .
.
- Calculer
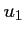 et
et 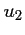 .
.
- On considère la suite
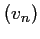 définie par
définie par
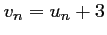 .
.
Montrer que la suite
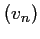 est géométrique.
est géométrique.
- En déduire une expression de
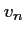 en fonction de
en fonction de 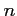 ,
puis de
,
puis de 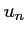 en fonction de
en fonction de 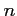 .
.
- Etudier les variations de la suite
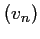 puis de la suite
puis de la suite
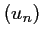 .
.
Correction
Correction
-
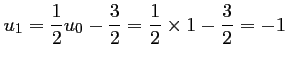 ;
;
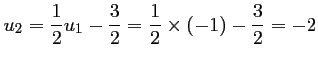 ;
;
-
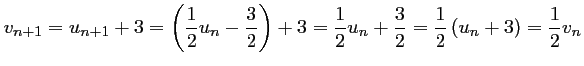 .
.
Ainsi, la suite
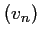 est géométrique de raison
est géométrique de raison 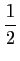 .
.
- On en déduit que pour tout entier naturel
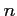 ,
,
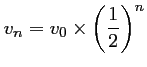 ,
avec
,
avec
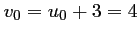 ,
d'où,
,
d'où,
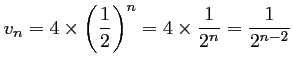 .
.
On a alors,
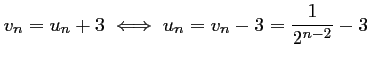 .
.
- Comme
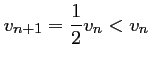 , la suite
, la suite 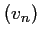 est
décroissante.
est
décroissante.
On a donc aussi,
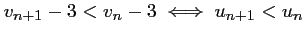 , et donc la
suite
, et donc la
suite 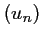 est aussi décroissante.
est aussi décroissante.
Tag:Suites
Voir aussi:
Quelques devoirs
variation d'une fonction composée avec une exponentielle - Deux inéquations avec des exponentielles - Suite numériques explicite et récurrente, construction graphique des premiers termes
Suites: construction graphique des premiers termes, suite intermédiaire arithmétique - Etude d'une suite récurrente avec une suite auxiliaire arithmétique
sur les suites: sommes des termes d'une suite arithmétique et géométrique. Etude d'une suite récurrente avec une suite auxiliaire. Suite récurrente définie avec une fonction exponentielle. Balle rebondissante: hauteur des rebonds et distance totales parcourue
fin d'année, sur les fonctions, exponentielle, suite et variable aléatoire
