Calcul sur les radicaux
Exercice corrigé - maths en seconde générale
Énoncé
Simplifier l'écriture de chacun des nombres suivants
(les fractions ne devront pas avoir de radical au dénominateur),
puis en déduire le plus petit ensemble (
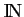 ,
,
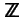 ,
,
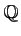 ou
ou
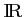 )
auquel il appartient :
)
auquel il appartient :
 ;
;
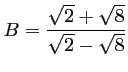 ;
;
 ;
;
 .
.
Correction
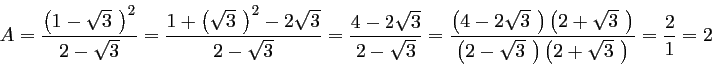
Correction
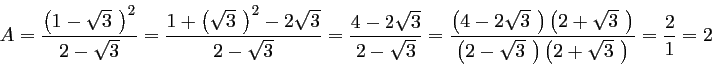
donc
![]() .
.
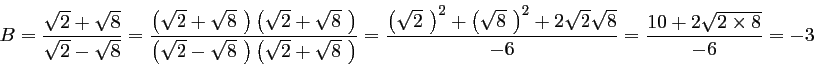
donc
![]() .
.
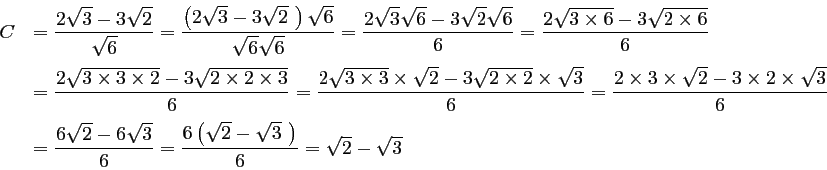
donc
![]() .
.
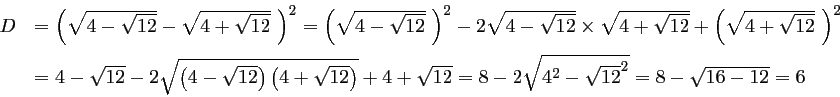
donc
![]() .
.
Tag:Calcul algébrique
Voir aussi:
Quelques devoirs
Interrogation sur les fraction et calcul algébrique: simplifier des fractions, mettre sur le même dénominateur
calcul algébrique: calculs avec des fractions, developper et factoriser des expressions algébriques, utiliser les identitées remarquables
calcul algébrique: factoriser des expressions algébriques, calculs avec des fractions: même dénominateur et écrire des fractions sans racine carrée au dénominateur
calcul algébrique: calculs avec des puissance, factoriser des expressions algébriques, et résoudre des premières équations
sur la résolution d'équations (produit nul, quotient nul, équation avec un carré) et deux fractions avec des puissances à simplifier
