Devoir de maths corrigé, Calcul algébrique, fractions, développer et factoriser
seconde
Devoir de mathématiques, et corrigé, sur les fractions, algébrique, développement et factorisation, posé en seconde générale, année scolaire 2024/2025
Exercice 1: Calcul numérique avec des fractions
Exprimer sous forme de fraction irréductible:
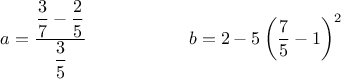
On calcule tout d'abord le numérateur, en mettant les fractions sur le même dénominateur, et ensuite en multiplie par l'inverse de la fraction au dénominateur:
![\[a=\frac{\displaystyle \frac{3}{7}-\frac{2}{5}}{\displaystyle \frac{3}{5}}
=\frac{\displaystyle \frac{1}{7\tm5}}{\displaystyle \frac{3}{5}}
=\frac{1}{7\tm5}\tm\frac{5}{3}
=\frac{1}{21}\]](/Generateur-Devoirs/2nde/Chap1/ex1_c/1.png)
On calcule tout d'abord le terme entre parenthèses:
![\[\begin{array}{ll}b&=2-5\lp\dfrac75-1\rp^2\\
&=2-5\lp\dfrac25\rp^2=2-5\tm\dfrac{2^2}{5^2}\\
&=2-\dfrac45=\dfrac65
\enar\]](/Generateur-Devoirs/2nde/Chap1/ex1_c/2.png)
Cacher la correction
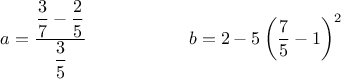
Correction exercice 1
On calcule tout d'abord le numérateur, en mettant les fractions sur le même dénominateur, et ensuite en multiplie par l'inverse de la fraction au dénominateur:
![\[a=\frac{\displaystyle \frac{3}{7}-\frac{2}{5}}{\displaystyle \frac{3}{5}}
=\frac{\displaystyle \frac{1}{7\tm5}}{\displaystyle \frac{3}{5}}
=\frac{1}{7\tm5}\tm\frac{5}{3}
=\frac{1}{21}\]](/Generateur-Devoirs/2nde/Chap1/ex1_c/1.png)
On calcule tout d'abord le terme entre parenthèses:
![\[\begin{array}{ll}b&=2-5\lp\dfrac75-1\rp^2\\
&=2-5\lp\dfrac25\rp^2=2-5\tm\dfrac{2^2}{5^2}\\
&=2-\dfrac45=\dfrac65
\enar\]](/Generateur-Devoirs/2nde/Chap1/ex1_c/2.png)
Cacher la correction
Exercice 2: Calcul algébrique avec des fractions
Ecrire les expressions suivantes sous la forme d'une seule fraction dont les numérateurs et dénominateurs seront développés:
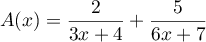 ;
;
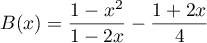 ;
;
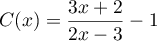
Exercice 3: Développer les expressions algébriques
Développer les expressions algébriques suivantes (réduire et ordonner les expressions développées suivant les puissances décroissantes de 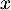 ):
):
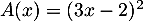 ;
; 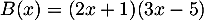 ;
; 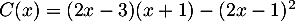
Exercice 4: Factoriser les expressions algébriques
Quelques autres devoirs
Interrogation sur les fraction et calcul algébrique: simplifier des fractions, mettre sur le même dénominateur
calcul algébrique: calculs avec des fractions, developper et factoriser des expressions algébriques, utiliser les identitées remarquables
calcul algébrique: factoriser des expressions algébriques, calculs avec des fractions: même dénominateur et écrire des fractions sans racine carrée au dénominateur
calcul algébrique: calculs avec des puissance, factoriser des expressions algébriques, et résoudre des premières équations
sur la résolution d'équations (produit nul, quotient nul, équation avec un carré) et deux fractions avec des puissances à simplifier
Quelques exercices corrigés
Exercices corrigés
Factorisations
Exercices corrigés
3 équations du 1er degré
Exercices corrigés
Factorisation, développement et résolution d'équations
Exercices corrigés
Vérification de la solution d'une équation - Calcul sur les radicaux et fractions
Exercices corrigés
Vérification de la solution d'une équation - Calcul sur les radicaux et fractions
Voir aussi:
![$\begin{array}{ll}C(x)&=2x^2+2x-3x-3-\bigl((2x)^2-2(2x)\tm1+1^2\bigr)\\[.5em]
&=2x^2-x-3-\bigl(4x^2-4x+1\bigr)\\[.5em]
&=-2x^2+3x-4\enar$](/Generateur-Devoirs/2nde/Chap1/ex9_c/3.png)
![$\begin{array}{ll}A(x)&=(2x+1)\Bigl[(x-3)+(5x+2)\Bigr]\\[.5em]
&=(2x+1)(6x-1)\enar$](/Generateur-Devoirs/2nde/Chap1/ex10_c/1.png)
![$\begin{array}{ll}B(x)&=(-x+3)\Bigl[(2x+1)-(x-4)\Bigr]\\[.5em]
&=(-x+3)\Bigl[2x+1-x+4\Bigr]\\[.5em]
&=(-x+3)(x+5)\enar$](/Generateur-Devoirs/2nde/Chap1/ex10_c/2.png)
![$\begin{array}{ll}C(x)&=\Bigl[(3x+1)-(x-2)\Bigr]\Bigl[(3x+1)+(x-2)\Bigr]\\[.5em]
&=\Bigl[2x+3\Bigr]\Bigl[4x-1\Bigr]\enar$](/Generateur-Devoirs/2nde/Chap1/ex10_c/3.png)
![$\begin{array}{ll}D(x)&=(x+3)\Bigl[(2x-5)-1\Bigr]\\[.5em]
&=(x+3)(2x-6)\enar$](/Generateur-Devoirs/2nde/Chap1/ex10_c/4.png)