Limite avec équivalents de ln, racine et exponentielle

Colle de mathématiques

Sujet de colle de maths:

Étudier la limite de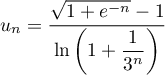

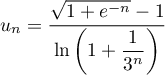
$u_n=\dfrac{\sqrt{1+e^{-n}}-1}{\ln\lp1+\dfrac1{3^n}\right)}$

Correction

Comme $e^{-n}\longrightarrow0$ , on a

$\sqrt{1+e^{-n}}\sim1+\dfrac12e^{-n}$

et donc pour le numérateur:

$\sqrt{1+e^{-n}}-1\sim\dfrac12e^{-n}$

Pour le dénominateur, on a

$\ln\lp1+\dfrac1{3^n}\rp\sim\dfrac1{3^n}$

et donc

$u_n\sim\dfrac123^ne^{-n}=\dfrac12\lp\dfrac3e\rp^n$

Comme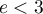

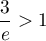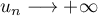, donc que $\dfrac3e>1$ on a alors $u_n\longrightarrow+\infty$ .

Autres sujets au hasard:

Voir aussi: