Suite arithmético-géométrique, somme des termes


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

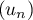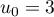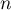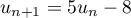Soit $(u_n)$ la suite définie par $u_0=3$ et, pour tout entier $n$, $u_{n+1}=5u_n-8$.
  1. Déterminer 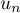$u_n$ en fonction de $n$.
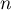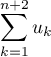
  2. Calculer $\dsp\sum_{k=1}^{n+2} u_k$



Correction

Correction

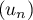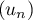  1. $(u_n)$ est une suite arithmético-géométrique. Si $(u_n)$ converge vers un réel 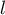$l$, celui-ci doit vérifier 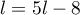$l=5l-8$, soit $l=2$.
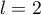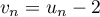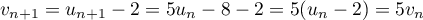    Soit $v_n=u_n-2$, alors $v_{n+1}=u_{n+1}-2=5u_n-8-2=5(u_n-2)=5v_n$.
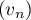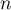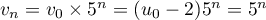    $(v_n)$ est donc géométrique et donc, pour tout entier $n$, $v_n=v_0\tm5^n=(u_0-2)5^n=5^n$.
    On trouve alors que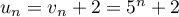 $u_n=v_n+2=5^n+2$.
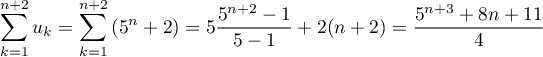
  2. $\dsp\sum_{k=1}^{n+2} u_k=\sum_{k=1}^{n+2}\lp5^n+2\right) =5\dfrac{5^{n+2}-1}{5-1}+2(n+2) =\dfrac{5^{n+3}+8n+11}{4}$


Tags:SuitesSommes

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0