Limite d'une racine n-ième

Colle de mathématiques

Sujet de colle de maths:

SuitesSuites
LimiteLimites de suites et de fonctions

Énoncé du sujet

Étudier la limite de la suite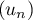

définie par $u_n=\sqrt[n]{n^2}$

Correction

On a $\ln\left( u_n\rp=\ln\left(\sqrt[n]{n^2}\rp =\dfrac1n\ln\left( n^2\right) =\dfrac{2}{n}\ln\left( n\rp$ .
Par croissances comparées, on sait que $\dsp\lim_{n\to+\infty}\dfrac{\ln(n)}{n}=0$ .
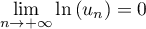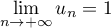Ainsi $\dsp\lim_{n\to+\infty}\ln\left( u_n\rp=0$ et donc $\dsp\lim_{n\to+\infty}u_n=1$ .

Tags:Suites Limite

Autres sujets au hasard:

Voir aussi: