Calculs de développements limités en a

Exercices corrigés et détaillés

Formules et méthode de calcul: DL usuels et changement de variable

Toutes les formules de DL sont connues en 0. Il faut bien sûr bien les connaître, et de plus savoir les adapter.
Deux cas se présentent en général:
  • On cherche le développement limité en a∈R.
    Pour x → a, on pose la nouvelle variable
    t = x − a
    et alors cette nouvelle variable tend bien vers 0.
  • On cherche le développement limité en l'infini: x → ±∞, on pose alors la nouvelle variable
    t = 1/x
    et cette nouvelle variable tend bien vers 0.
On exprime toute l'expression, ou la fonction, seulement en fonction de cette nouvelle variable et on peut alors utiliser les formules de DL en 0.

Exercices corrigés: calculer les développements limités

Calculer les développements limités en a des fonctions suivantes, au point donné et à l'ordre indiqué.

  1. f (x) = x + 2x + 3 + x en 1 à l'ordre 2
    f(x) = 1 + 7/4(x−1) − 15/64(x−1)2 + o((x−1)2)
    Pour obtenir le développement limité en 1, à l'ordre 2, on se ramène à 0 en posant $u=x-1\iff x=u+1$, et on a alors

    \[\begin{array}{lcl}f(x)&=&x+2\sqrt{x}-\sqrt{3+x}\\ &=&u+1+2\sqrt{u+1}-\sqrt{4+u}\\[1em] &=&u+1+2\sqrt{1+u}-\sqrt{4\lp1+\dfrac{u}4\right)}\\[1em] &=&u+1+2(1+u)^{1/2}-2\lp1+\dfrac{u}4\rp^{1/2}\\[1em] &=&u+1+2\lp1+\dfrac12u-\dfrac18u^2+o\lp u^2\rp\rp \\[1em]&&-2\lp1+\dfrac18u-\dfrac18\lp\dfrac{u}4\rp^2+o\lp u^2\rp\rp\\[1.4em] &=&1+\dfrac74u-\dfrac{15}{64}u^2+o\left( u^2\right) \enar\]


    et on trouve donc, en revenant à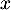 $x$, le développement limité en 1:
    \[f(x)=1+\dfrac74(x-1)-\dfrac{15}{64}(x-1)^2+o\left( (x-1)^2\rp\]

  2. f (x) = ecos(x) en π/2 à l'ordre 2
    f(x) = 1 − (x−π/2) + 1/2 x−π/2 2 + o x−π/2 2
    On se ramène au DL en 0 en posant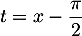 $t=x-\dfrac\pi2$.
    On a alors
    \[\begin{array}{ll}\cos(x)&=\cos\left( t+\dfrac\pi2\rp\\[.5em]&=-\sin(t)\\[.5em]&=t+o(t^2)\enar\]

    et donc
    \[\begin{array}{ll}f(x)&=e^{-\sin(t)} =e^{-t+o(t^2)}\\ &=1+\lp-t+o(t^2)\rp+\dfrac{\lp-t+o(t^2)\rp^2}{2!}+o(t^2)\\ &=1-t+\dfrac{t^2}2+o(t^2) \enar\]

    et enfin, en revenant à la variable de départ,
    \[f(x)=1-\left( x-\dfrac\pi2\rp+\dfrac{\left( x-\dfrac\pi2\rp^2}2 + o\left(\left( x-\dfrac\pi2\rp^2\rp\]

  3. f (x) = x + 1/x2 en 1 à l'ordre 2
    f(x) = 2 + 72/4(x−1) + 792/32(x−1)2 + o((x−1)2)
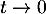    On pose $t=x-1\iff x=t+1$ et alors $t\to0$ et
    \[f(x)=\dfrac{\sqrt{2+t}}{(1+t)^2} =\sqrt2\lp1+\dfrac{t}2\rp^{1/2}(1+t)^{-2}\]

    On a alors
    \[\lp1+\dfrac{t}2\rp^{1/2}=1+\dfrac{t}4-\dfrac{t^2}{32}+o(t^2)\]

    et
    \[(1+t)^{-2}=1-2t+3t^2+o(t^2)\]

    puis le produit
    \[f(x)=\sqrt2\lp1+\dfrac{t}4-\dfrac{t^2}{32}+o(t^2)\rp\lp1-2t+3t^2+o(t^2)\rp\]

    soit, en développant et en ne gardant que les termes de degré au plus 2,
    \[f(x)=\sqrt2\lp1-\dfrac74t+\dfrac{79}{32}t^2+o(t^2) \rp\]

    ou encore, en revant à la variable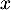 $x$,
    \[f(x)=\sqrt2-\dfrac{7\sqrt2}{4}(x-1)+\dfrac{79\sqrt2}{32}(x-1)^2+o((x-1)^2)\]

  4. f (x) = e1/x−1 en 1 à l'ordre 1
    f(x) = e − e/2(x−1) + o(x−1)
    On pose $t=x-1\to0$ et alors,
    \[f(x)=(1+t)^{1/t}=e^{\frac1t\ln(1+t)}\]

    où
    \[\ln(1+t)=t-\dfrac{t^2}2+o(t^2)\]

    et alors en divisant par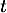 $t$,
    \[\dfrac1t\ln(1+t)=1-\dfrac{t}2+o(t)\]

    puis l'exponentielle,
    \[\begin{array}{ll}e^{\frac1t\ln(1+t)} &=e^{1-\dfrac{t}2+o(t)}\\ &=e\,e^{-\dfrac{t}2+o(t)}\\ &=e\lp1+\lp-\dfrac{t}2+o(t)\rp+o(t)\rp\\ &=e-\dfrac{et}2+o(t) \enar\]

    et finalement, en revenant à la variable de départ:
    \[f(x)=e-\dfrac{e}2(x-1)+o(x-1)\]

  5. f (x) = x/1 + ex en +∞ à l'ordre 2
    f(x) = x/2 − 1/4 + 1/48x2 + o1/x2
    On pose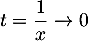 $t=\dfrac1x\to0$ lorsque 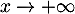$x\to+\infty$ et alors
    \[f(x)=\dfrac{1/t}{1+e^t}=\dfrac1t\tm\lp1+e^t\rp^{-1}\]


    On a alors
    \[e^t=1+t+\dfrac{t^2}2+\dfrac{t^3}6+o\left( t^3\rp\]

    et donc
    \[(1+e^t)^{-1}=(2+u)^{-1}=2^{-1}\lp1+\dfrac{u}2\rp^{-1}\]

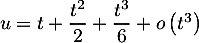    avec $u=t+\dfrac{t^2}2+\dfrac{t^3}6+o\left( t^3\rp$ et $u\to0$.
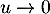    On a alors
    \[\begin{array}{ll}\lp1+\dfrac{u}2\rp^{-1}&=1-\dfrac{u}2+\lp\dfrac{u}2\rp^2 -\lp\dfrac{u}2\rp^3+o\lp u^3\rp\\[1em] &=1-\dfrac{u}2+\dfrac{u^2}4-\dfrac{u^3}8+o\left( u^3\right) \enar\]

    et en revenant à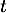 $t$,
    \[\begin{array}{lll}\lp1+\dfrac{u}2\rp^{-1} &=1&-\dfrac12\left( t+\dfrac{t^2}2+\dfrac{t^3}6+o\left( t^3\rp\rp\\[1em] &&+\dfrac14\left( t+\dfrac{t^2}2+\dfrac{t^3}6+o\left( t^3\rp\rp^2\\[1em] &&-\dfrac18\left( t+\dfrac{t^2}2+\dfrac{t^3}6+o\left( t^3\rp\rp^3 + o(t^3) \enar\]

    puis en ne gardant que les termes de degré inférieur ou égal à 3,
    \[\begin{array}{lll}\lp1+\dfrac{u}2\rp^{-1} &=1&-\dfrac12\left( t+\dfrac{t^2}2+\dfrac{t^3}6+o\left( t^3\rp\rp\\[1em] &&+\dfrac14\left( t^2+2\times t\times\dfrac{t^2}2\rp\\[1em] &&-\dfrac18\left( t^3\right) + o(t^3) \enar\]

    soit
    \[\lp1+\dfrac{u}2\rp^{-1} =1 -\dfrac12t +\lp-\dfrac1{12}+\dfrac14-\dfrac18\right) t^3+o(t^3) \]

    c'est-à-dire
    \[\lp1+\dfrac{u}2\rp^{-1} = 1-\dfrac12t+\dfrac1{24}t^3+o(t^3) \]

    d'où
    \[(1+e^t)^{-1}=2^{-1}\lp1+\dfrac{u}2\rp^{-1} =\dfrac12-\dfrac14t+\dfrac1{48}t^3+o(t^3)\]


    On revient finalement à notre fonction de départ:
    \[f(x)=\dfrac1t(1+e^t)^{-1} =\dfrac1{2t}-\dfrac14+\dfrac1{48}t^2+o(t^2)\]

    et donc, comme $t=\dfrac1x\iff x=\dfrac1t$,
    \[f(x)=\dfrac{x}2-\dfrac14+\dfrac1{48x^2}+o\lp\dfrac1{x^2}\rp\]


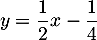    On en déduit l'équation de l'asymptote oblique à la courbe de $f$, à savoir $y=\dfrac12x-\dfrac14$, et que, comme
    \[f(x)-\lp\dfrac12x-\dfrac14\rp=\dfrac1{48x^2}+o\lp\dfrac1{x^2}\rp\]

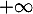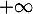    est positif au voisinage de $+\infty$, que la courbe de $f$ est au-dessus de son asymptote au voisinage de $+\infty$.

Voir aussi:
LongPage: h2: 3 - h3: 0