Suite récurrente du 2nd degré
Exercice corrigé - Spécialité maths, première générale
Énoncé
Soit la fonction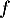 
définie sur 
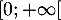par l'expression
.
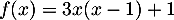On note de plus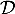
la droite d'équation 
.
définie sur par l'expression
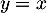. On note de plus
la droite d'équation .
- Donner le tableau de variation de
.
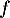- Déterminer les coordonnés des éventuels points d'intersection
de
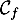et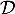 
.
- Tracer
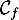dans un repère orthonormal.
On prendra 1 unité = 10 cm.
- On définit la suite
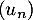par
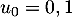puis, pour tout entier 
,
.
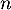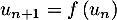Construire sur l'axe des abscisses les premiers termes de la suite,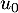
, 
, 
, … , 
.
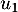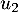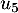Correction
Correction
-
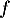est une fonction du second degré,
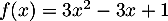avec 
,
avec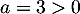 
et 
,
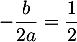donc,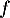 
est décroissante sur ![$\Bigl]-\infty;\dfrac12\Bigr]$](/Generateur-Devoirs/1S/Chap9/exSRsdg_c/6.png)
et est croissante sur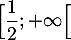 
.
Le minimum de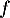
est de plus
.
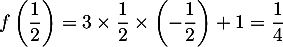- Soit
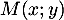un éventuel point d'intersection de
et 
,
alors, 
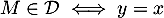et,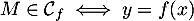 
.
On doit donc avoir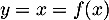
, soit en particulier
.
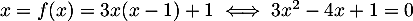On peut calculer le discriminant, ou s'apercevoir que ce trinôme admet 1 comme racine évidente, et donc trouver que les racines de cette équations son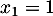t
et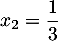 
.
Ainsi, il y a deux points d'intersection: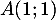
et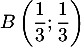 
.
-
![\[\psset{unit=10cm,arrowsize=7pt}
\begin{pspicture*}(-.2,-.2)(1.2,1.2)
\psline{->}(-0.2,0)(1.2,0)
\psline{->}(0,-0.2)(0,1.2)
\psline(1,-0.01)(1,0.01)%
\psline(-0.01,1)(0.01,1)%
\rput(-0.03,1){1}%
\rput(1,-0.03){1}%
\rput(0.333,0.333){\large\bf$\tm$}\rput(0.37,0.34){$A$}
\rput(1,1){\large\bf$\tm$}\rput(1.04,1){$B$}
% Definition de la fonction f de u_{n+1}=f(u_n)
\newcommand{\f}[1]{3 #1 mul #1 1 sub mul 1 add}
% Et son tracer:
\psplot[linewidth=1.4pt,plotpoints=500]{-.1}{1.2}{\f{x}}
% ainsi que le tracer de la droite y=x
\psplot{-0.2}{1.2}{x}
% Defintion de la fonction it\'er\'ee:
% par ex.: fn{3}{x}=f(f(f(x)))
\newcommand\fn[2]{%
\ifnum#1=1
\f{#2}%
\else
\f{\fn{\numexpr#1-1}{#2}}%
\fi
}
% Valeur initiale (u_0)
\def\xinit{0.1}
\def\nmax{5}
% Initialisation pour u_0
\psline[linestyle=dashed]
(\xinit,0)
(!\xinit\space\f{\xinit})
(!\f{\xinit}\space\f{\xinit})
\rput(\xinit,-0.05){$u_0$}
% Boucle pour u_1, u_2, ..., u_nmax
\multido{\i=1+1}{\nmax}{
\psline[linestyle=dashed]
(!\fn{\i}{\xinit} \space 0)
(!\fn{\i}{\xinit} \space \fn{\i}{\xinit})
(!\fn{\i}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
(!\fn{\numexpr\i+1}{\xinit} \space \fn{\numexpr\i+1}{\xinit})
\rput(!\fn{\i}{\xinit}\space 0){$\tm$}
\rput(!\fn{\i}{\xinit}\space -0.05){$u_\i$}
}
\end{pspicture*}\]](/Generateur-Devoirs/1S/Chap9/exSRsdg_c/21.png)
Tags:Suites2nd degré
Autres sujets au hasard:
Voir aussi: