Second degré et polynômes

Résolution d'équation, inéquations et problèmes du second degré

Anglais

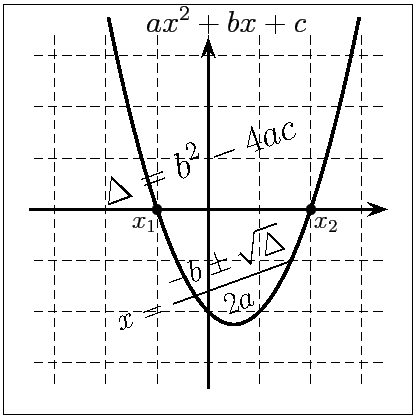
$\displaystyle \begin{pspicture}(-4,0)(4,4)\psset{unit=1cm,arrowsize=8pt}\ps... ...t(2.3,-0.3){\large$x_2$}%\rput(0.35,3.7){\Large$ax^2+bx+c$}\end{pspicture}$

Trinôme du second degré

Equations du second degré


Définition
On appelle trinôme du second degré toute expression de la forme ax2 + bx + c , où a, b et c, sont trois nombres réels quelconques, et a ≠ 0.

Exemple: de trinômes du second degré:

Trinômes a b c
P(x) = 3x2 + 2x −5 3 2 −5
Q(x) = 2x2 − 3x + 23 2 −3 23
R(x) = −x2 + 52x −1 52 0
S(x) = x2 + (1−2)x − π 1 1−2 − π
T(x) = 65x2 − 3 65 0 −3
U(x) = (x − 2)2 + 3(x + 3) 1 −1 13


Définition
On appelle discriminant du trinôme du second degré ax2 + bx + c , le nombre, noté Δ, et défini par:
Δ = b2 − 4ac

Exemples: de discriminant de trinômes du second degré:
Trinômes   a     b     c     Δ  
P(x) = 3x2 + 2x −5 3 2 −5 64
Q(x) = x2 + 2x + 1 1 2 1 0
R(x) = x2 − 2x − 5 1 2 −5 22


Propriété
On considère l'équation (E): ax2 + bx + c = 0 avec a ≠ 0 et de discriminant Δ = b2 − 4ac.
  • Si Δ > 0, l'équation (E) admet deux solutions distinctes (aussi appelées racines):
    x1 = −b − Δ 2a x2 = −b + Δ 2a
  • Si Δ = 0, l'équation (E) admet une unique solution (ou racine) double:
    x0 = −b 2a
  • Si Δ < 0, l'équation (E) n'admet aucune solution réelle.


Exercice 1
Déterminer les solutions des équations:
a) x2 − 2x + 1 = 0

b) x2 − 1 = 0

c) 4x2 + 8x − 5 = 0

d) 3x2 + x + 6 = 0


Signe d'un trinôme du second degré

Propriété
Soit f (x) = ax2 + bx + c avec a ≠ 0, alors,
  • Si Δ > 0, et x1 et x2 sont les deux racines alors
    x −∞ x1 x2 +∞
    f Signe de a 0 Signe de −a 0 Signe de a

  • Si Δ = 0 et x0 est la racine double alors,
    x −∞ x1 +∞
    f Signe de a 0 Signe de a

  • Si Δ < 0, le trinôme n'a pas de racine et il est donc toujours du même signe,
    x −∞ +∞
    f Signe de a


Exercice 2
Étudier le signe de:
a) P(x) = x2 − 2x + 1

b) Q(x) = x2 − 1

c) R(x) = −3x2 + 5x − 2

d) S(x) = 2x2 + x + 3

Exercices

Exercice 3
Résoudre les inéquations:
a) x2 − 2x + 1 > 0


b) −3x2 + 5x − 2 ≤ 0


c) x(2x − 5) ≥ x − 6



Exercice 4
Etudier le signe de:
a) f (x) = −x2 + x −3

b) g(x) = x − 1x



c) h(x) = 2x + 4x − 3

QCM: Résolution d'équations et inéquations du 2nd degré Lien vers les exercices corrigés

Exercice 5 (Équations bicarrées)
En effectuant le changement de variable X = x2 résoudre les équations:

a) x4 − 13x2 + 36 = 0

b) x2 + 1x2 − 6 = 0


Exercice 6
Déterminer les points d'intersection (s'ils existent) de la parabole P et de la droite D d'équations: P: y = x2 − 3x + 1 et D: y = −2x + 1

Exercice 7
Déterminer les points d'intersection des paraboles P et P' d'équations P: y = x2 − x + 2 et P': y = −x2 + 2x − 6


Exercice 8
Soit m un nombre réel. On considère l'équation     4x2 + (m − 1)x + 1 = 0
Déterminer m pour que cette équation admette une unique solution.
Déterminer alors cette solution.


Polynômes



Voir aussi:

LongPage: h2: 1 - h3: 2