Sens de variation d'une suite définie par une fonction
Exercice corrigé - Spécialité maths, première générale
Énoncé
Étudier le sens de variation de la suite 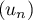 définie par
définie par
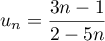 pour tout entier naturel
pour tout entier naturel 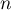 .
.
Correction
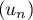 est définie explicitement par
est définie explicitement par
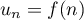 avec la fonction
avec la fonction 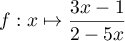 définie sur
définie sur 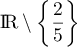 .
.
On a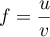 avec
avec
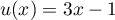 donc
donc 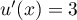 et
et 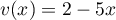 donc
donc 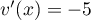 .
.
On a alors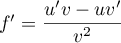 ,
soit
,
soit
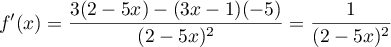 .
.
Comme pour tout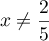 , on a
, on a
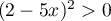 , on a aussi
, on a aussi 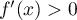 ,
et donc
,
et donc 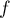 est strictement croissante sur
est strictement croissante sur
![$\Bigl]-\infty;\dfrac25\Bigr[$](/Generateur-Devoirs/1S/Chap9/ex2.2_c/16.png) et sur
et sur
![$\Bigl]\dfrac25;+\infty[$](/Generateur-Devoirs/1S/Chap9/ex2.2_c/17.png) .
.
La suite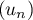 est donc strictement croissante pour
est donc strictement croissante pour 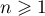 .
.
Remarque: on ne sait pas si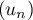 est croissante sur
est croissante sur 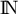 tout entier.
D'ailleurs ici, calculs faits, on s'aperçoit du contraire:
tout entier.
D'ailleurs ici, calculs faits, on s'aperçoit du contraire:
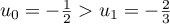
Correction
La suiteOn a
On a alors
Comme pour tout
La suite
Remarque: on ne sait pas si
Tag:Suites
Voir aussi:
