Vélo ou bus pour se rendre au lycée

Exercice corrigé - Spécialité maths, première générale

Énoncé

Un élève doit se rendre à son lycée chaque matin pour 8h00. Pour cela, il utilise, selon les jours, deux moyens de transport : le vélo ou le bus.
L'élève part tous les jours à 7h40 de son domicile et doit arriver à 8h00 à son lycée. Il prend le vélo 7 jours sur 10 et le bus le reste du temps.
Les jours où il prend le vélo, il arrive à l’heure dans 99,4% des cas et lorsqu’il prend le bus, il arrive en retard dans 5% des cas.
On choisit une date au hasard en période scolaire et on note les événements
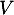$V$: « L'élève se rend au lycée à vélo»
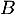$B$: « l'élève se rend au lycée en bus»
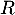$R$: « L’élève arrive en retard au lycée».
  1. Traduire la situation par un arbre de probabilités.
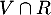  2. Déterminer la probabilité de l’événement $V\cap R$.
  3. Démontrer que la probabilité de l’événement R est 0,0192
  4. Un jour donné, l'élève est arrivé en retard au lycée. Quelle est la probabilité qu'il s'y soit rendu en bus ?



Correction

Correction


  1. \[\psset{xunit=1cm,yunit=.6cm} \begin{pspicture}(-2,-3)(5,2.) \psline(0,0)(1.5,1.5)\rput(1.75,1.5){$V$}\rput(.7,1.3){$7/10$} \psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$R$}\rput(2.7,2.3){$0,6\%$} \psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{R}$}\rput(2.7,.6){$99,4\%$} \psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$B$}\rput(.7,-1.3){$3/10$} \psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$R$}\rput(2.7,-.6){$5\%$} \psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{R}$}\rput(2.7,-2.4){$95\%$} \end{pspicture}\]

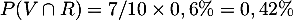
  2. $P(V\cap R) = 7/10\tm0,6\%=0,42\%$
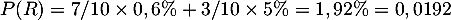
  3. D'après la formule des probabilités totales, $P(R)= 7/10\tm0,6\% + 3/10\tm5\% = 1,92\% = 0,0192$
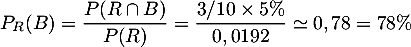
  4. On cherche la probabilité conditionnelle $P_R(B)=\dfrac{P(R\cap B)}{P(R)}=\dfrac{3/10\tm5\%}{0,0192} \simeq 0,78 = 78\%$


Tag:Probabilités conditionnelles

Autres sujets au hasard: Lancer de dés


Voir aussi:
LongPage: h2: 3 - h3: 0