Géométrie dans l'espace
Produit scalaire dans l'espace
Exercice 10
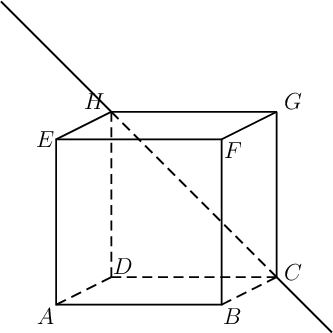
Déterminer le projeté orthogonal
(Indication: quelle est la nature du triangle
Exercice 11
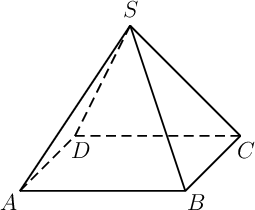
Calculer, en fonction de
Exercice 12
- Calculer, en fonction de
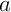 , les produits scalaires:
, les produits scalaires:
-
- Déterminer dans le repère
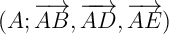 les
coordonnées de tous les points et retrouver a).
les
coordonnées de tous les points et retrouver a). - Déterminer une mesure de l'angle
 .
.
Exercice 13
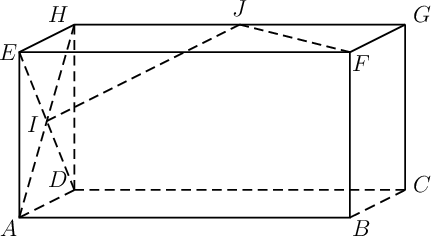
- Donner, dans le RON
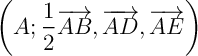 ,
les coordonnées des points
,
les coordonnées des points 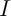 ,
, 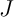 et
et 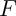 .
.
En déduire le produit scalaire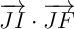 .
.
- Déterminer l'angle, au dixième de degré près,
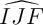 .
.
Exercice 14
Calculer
Orthogonalité dans l'espace
Voir aussi: