Produit scalaire et géométrie analytique du plan
On se place dans toute la suite dans un repère orthonormal
Expression du produit scalaire
Propriété
Soit dans un repère orthonormal,
Remarque: On a alors aussi,
Exercices
Exercice 1
- Soit
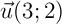 et
et 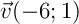 .
Calculer le produit scalaire
.
Calculer le produit scalaire 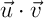 et les normes
et les normes 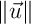 et
et 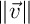 .
.
En déduire l'angle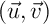 .
.
- Soit
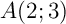 ,
, 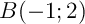 et
et 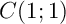 .
.
Calculer le produit scalaire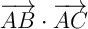 , puis
les normes
, puis
les normes 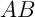 et
et 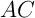 .
.
En déduire l'angle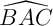 .
.
Exercice 2
Dans un RON, on considère les points Donner une valeur de
Exercice 3
Dans un RON (repère orthonormal), on considère les points
- Faire une figure.
- Calculer l'angle
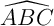 .
. - Calculer la longueur
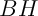 .
.
Exercice 4
Soit ![\[\psset{unit=1.2cm}
\begin{pspicture}(-0.5,-0.4)(3,2.9)
\pspolygon(0,0)(2.5,0)(2.5,2.5)(0,2.5)
\rput(-0.2,2.7){$A$}\rput(2.7,2.7){$B$}
\rput(2.7,-0.2){$C$}\rput(-0.2,-0.2){$D$}
\psline(0,2.5)(2.5,2)\rput(2.7,2){$I$}
\psline(2,0)(2.5,2.5)\rput(1.9,-0.25){$J$}
\end{pspicture}\]](Cours-analytique-IMG/95.png)
En utilisant le repère orthonormal
Voir aussi: