Géométrie dans l'espace

Intersection de trois plans


Propriété
Soit $\mathcal{P}$ et $\mathcal{L}$ et $\mathcal{R}$ trois plans de l'espace. Alors, six cas sont possibles:
  1. Ils n'ont aucun point commun:
    1. Les trois plans sont strictement parallèles
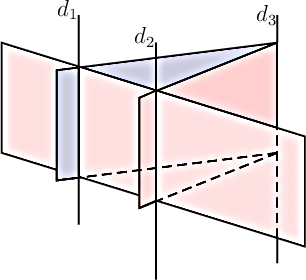
      pspicture...


    2. Deux plans sont strictement parallèles et sécants au troisième
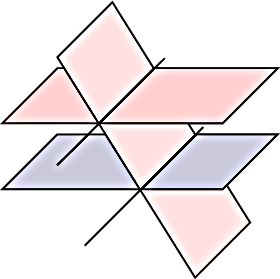
      pspicture...


    3. Deux plans sont sécants suivant une droite, et le troisième plan est strictement parallèle à cette droite est un plan
      pspicture...


  2. Ils ont un unique point d'intersection

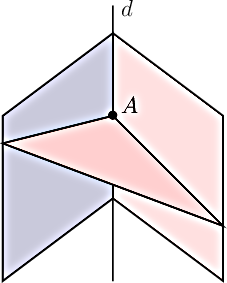
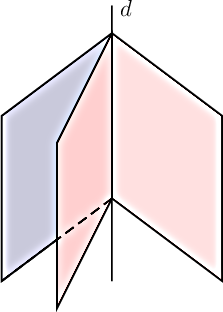
    pspicture...


  3. Leur intersection est une droite

    pspicture...


  4. Leur intersection est un plan: les trois plans sont confondus
    pspicture...




Propriété
Algébriquement, si dans un RON, les plans ont pour équations respectives $ax+by+cz+d=0$, $a'x+b'y+c'z+d'=0$, et $a''x+b''y+c''z+d''=0$, alors leur intersection est l'ensemble des points $M(x;y;z)$ tels que:
\[\la\bgar{ccccccccc} ax &+& by &+& cz &+& d &=& 0\\ a'x &+& b'y &+& c'z &+& d'&=& 0\\ a''x &+& b''y &+& c''z &+& d''&=& 0 \enar\right.\]

Ce système de trois équations à trois inconnues peut donc avoir: aucune solution (cas 1.), une unique solution (cas 2.), ou une infinité (cas 3. ou 4.).



Exercice 22
Déterminer l'intersection des plans $\mathcal{P}$, $\mathcal{L}$ et $\mathcal{R}$ d'équations respectives:
\[\mathcal{P}: 3x+3y+z+2=0\]


\[\mathcal{L}: y+z-5=0\]

et
\[\mathcal{R}: 2z-8=0\]


Exercice 23
Déterminer l'intersection des plans $\mathcal{P}$, $\mathcal{L}$ et $\mathcal{R}$ d'équations respectives:
\[\mathcal{P}: 4x+3y+z+2=0\]


\[\mathcal{L}: x+2y+z-5=0\]

et
\[\mathcal{R}: 3x+5y+2z-9=0\]




Voir aussi:
LongPage: h2: 2 - h3: 0