Géométrie dans l'espace


Coordonnées, vecteurs et géométrie analytique dans l'espace

Vecteurs coplanaires


Définition
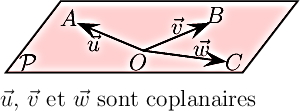
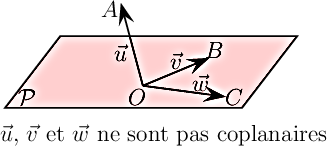
Dire que les vecteurs $\vec{u}$, $\vec{v}$, et $\vec{w}$ sont coplanaires signifie qu'ils peuvent être placés dans un même plan: les points $O$, $A$, $B$ et $C$ tels que $\V{OA}=\vec{u}$, $\V{OB}=\vec{v}$ et $\V{OC}=\vec{w}$ sont dans un même plan.
\begin{pspicture}...\end{pspicture}


\begin{pspicture}...\end{pspicture}


Propriété
Les vecteurs $\vec{u}$, $\vec{v}$ et $\vec{w}$ sont coplanaires si et seulement si il existe des réels $a$ et $b$ tels que $\vec{u}=a\vec{v}+b\vec{w}$.

Exercice 3
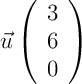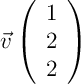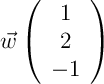Les vecteurs $\vec{u}\lp\bgar{c} 3\\6\\0\enar\rp$, $\vec{v}\lp\bgar{c} 1\\2\\2\enar\rp$ et $\vec{w}\lp\bgar{c} 1\\2\\-1\enar\rp$ sont-ils coplanaires ?


Exercice 4
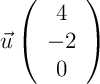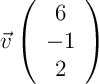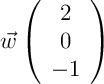Les vecteurs $\vec{u}\lp\bgar{c} 4\\-2\\0\enar\rp$, $\vec{v}\lp\bgar{c} 6\\-1\\2\enar\rp$ et $\vec{w}\lp\bgar{c} 2\\0\\-1\enar\rp$ sont-ils coplanaires ?



Voir aussi:
LongPage: h2: 1 - h3: 3