Géométrie dans l'espace
Orthogonalité dans l'espace
Orthogonalité de deux droites
Définition
- Deux droites sont orthogonales si leurs parallèles menées par un point quelconque sont perpendiculaires.
- Deux droites sont orthogonales si et seulement si leurs directions, et donc vecteurs directeurs, sont orthogonaux.
- Deux droites de l'espace sont perpendiculaires si et seulement si elles sont orthogonales et sécantes.
Remarque: Dans l'espace, deux droites peuvent n'être ni parallèles ni sécantes (par exemple, les droites
Exemple/Exercice
Les droites ![\[d: \la\bgar{rcrcr}
x&=&3&+&2t \\
y&=&2&-&3t\\
z&=&1&-&t
\enar\right.,\ t\in\R\]](Cours-IMG/362.png)
et,
![\[d': \la\bgar{rcrcr}
x&=&4&+&3t \\
y&=&-5&+&t\\
z&=&-4&+&3t
\enar\right.,\ t\in\R\]](Cours-IMG/363.png)
Correction
Un vecteur directeur de ce qui montre que ces vecteurs sont orthogonaux, comme les deux droites qu'ils dirigent.
Pour que ces droites soient perpendiculaires, il faut aussi qu'elles soient sécates. On cherche s'il existe un point
![\[d: \la\bgar{cccrrrrcrcr}
x&=&3&+&2t&=&4&+&3t' \\
y&=&2&-&3t&=&-5&+&t'\\
z&=&1&-&t&=&-4&+&3t'
\enar\right.,\ t\in\R\]](Cours-IMG/372.png)
La deuxième équation se réécrit
![\[\bgar{rll}&3+2t&=4+3t'\\
&&=4+3(7-3t)\\
\iff&11t&=22 \\
\iff&t&=2\enar\]](Cours-IMG/374.png)
On en déduit que
On a donc trouvé que ces deux droites sont perpendiculaires en
Droites et plans perpendiculaires
Définition
Une droite est perpendiculaire à un plan lorsqu'elle est orthogonale à
toutes les droites de ce plan.
(3,0)(4,1)(1,1)](Cours-IMG/377.png)
La définition précédente parle de l'orthogonalité avec toutes ls droites du plan, c''est-à-dire de l'orthogonalité à une infinité de droites.
En fait, un plan se défini à partir de seulement deux directions, ou vecteurs, et on peut donc résumer cette infinité de droites à seulement deux.
Propriété
Une droite est perpendiculaire à un plan si et seulement si
elle est othogonale à deux vecteurs non colinéaires de ce plan.
Démonstration
- La condition est nécessaire.
Si
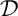 est perpendiculaire à
est perpendiculaire à 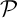 , elle est orthogonale à toutes les droites de
, elle est orthogonale à toutes les droites de 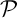 .
.
En particulier, il existe deux droites de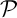 , non parallèles et orthogonales à
, non parallèles et orthogonales à 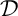 et
et 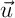 est donc orthogonal aux vecteurs directeurs de ces droites qui sont des vecteurs de
est donc orthogonal aux vecteurs directeurs de ces droites qui sont des vecteurs de 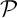 non colinéaires.
non colinéaires. - Réciproque: la condition est suffisante.
Soit
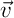 et
et 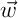 deux vecteurs non colinéaires de
deux vecteurs non colinéaires de 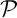 orthogonaux à
orthogonaux à 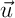 .
.
Alors, pour tout vecteur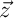 de
de 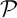 , les vecteurs
, les vecteurs 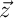 ,
, 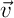 et
et 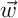 sont coplanaires, et donc, il existe
sont coplanaires, et donc, il existe 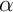 et
et 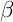 tels que
tels que
![\[\vec{z}=\alpha\vec{v}+\beta\vec{w}\]](Cours-IMG/396.png)
et on a alors,
![\[\bgar{ll}\vec{u}\cdot\vec{z}
&=\vec{u}\cdot\lp \alpha\vec{v}+\beta\vec{w}\rp\\
&=\alpha\vec{u}\cdot\vec{v}+\beta\vec{u}\cdot\vec{w}\\
&=0\enar\]](Cours-IMG/397.png)
ce qui montre que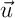 et
et 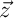 sont orthogonaux, et donc,
sont orthogonaux, et donc,
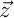 étant un vecteur quelconque de
étant un vecteur quelconque de 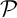 , que
, que 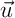 est orthogonal à tout vecteur de
est orthogonal à tout vecteur de 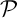 .
.
Exercice 15
On considère dans un RON, les points Montrer que le vecteur
Vecteur normal à un plan et plans perpendiculaires
Propriété
Soit 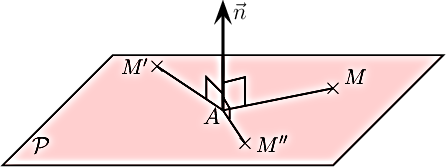
On obtient ainsi l'équation cartésienne d'un plan dans l'espace, complètement analogue à l'équation cartésienne d'une droite dans le plan de vecteur normal donné.
Corollaire
Dans un repère orthonormal,
le vecteur Démonstration
Soit Et enfin, comme pour l'orthogonalité de deux droites, pour deux plans il suffit de regarder leurs vecteurs orthogonaux:
Définition
Deux plans sont orthogonaux si et seulement leurs vecteurs normaux
le sont.
Exercice 16
L'espace est muni d'un RON - Déterminer une équation cartésienne du plan
 tel que le projeté orthogonal de l'origine
tel que le projeté orthogonal de l'origine  sur
sur  soit le point
soit le point 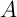 .
.
- Montrer que les plans
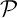 et
et 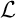 sont
perpendiculaires.
sont
perpendiculaires.
Exercice 17
Dans un RON, le plan - Déterminer les coordonnées d'un vecteur
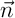 normal à
normal à
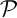 .
.
- Justifier l'existence d'un réel
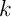 tel que
tel que
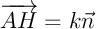 .
.
Traduire cette relation en termes de coordonnées.
- Déterminer
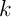 en exprimant que
en exprimant que 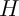 appartient à
appartient à
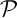 .
.
En déduire les coordonnées de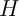 et la distance
et la distance 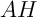 de
de 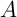 au plan
au plan 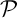 .
.
Intersection de plans et de droites dans l'espace
Voir aussi: