Géométrie dans l'espace
Coordonnées, vecteurs et géométrie analytique dans l'espace
Deux exercices pour se repérer
Vecteurs coplanaires
Représentation paramétrique d'une droite dans l'espace
Dans l'espace, le principe de la repésentation paramétrique d'une droite est la même que pour la représentation paramétrique de droite du plan.Définition
La droite Autrement dit,
![\[\la\bgar{ll}
x=x_A+ta \\
y=y_A+tb \\
z=z_A+tc
\enar\right.\ , \ t\in\R\]](Cours-IMG/116.png)
(ou "
Le système précédent est une représentation paramétrique de la droite
Exercice 5
On considère la droite - Donner un vecteur directeur
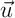 de la droite
de la droite 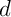 .
.
- Donner alors une représentation paramétrique de la droite
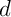 .
.
- Les points
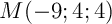 et
et 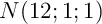 appartiennent-ils à cette
droite ?
appartiennent-ils à cette
droite ?
Exercice 6
On donne les points - Déterminer une représentation paramétrique de la droite
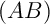 .
.
- Les points
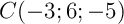 et
et 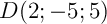 appartiennent-ils à cette droite ?
appartiennent-ils à cette droite ?
Exercice 7
Les droites ![\[d: \la\bgar{cccccl}
x&=&2t &-& 1 \\
y&=&-3t &+& 2\\
z&=&t &&
\enar\right.,\ t\in\R\]](Cours-IMG/158.png)
et,
![\[d': \la\bgar{cccccl}
x&=&3t && \\
y&=&t &+& 2\\
z&=&-3t &-& 2
\enar\right.,\ t\in\R\]](Cours-IMG/159.png)
Exercice 8
Démontrer que les droites ![\[d: \la\bgar{cccccl}
x&=&5 &+& 3t \\
y&=&2 &+& t\\
z&=&1 &-& 4t
\enar\right.,\ t\in\R\]](Cours-IMG/165.png)
et,
![\[d': \la\bgar{cccccl}
x&=&-11 &+& 2t \\
y&=&10 &-& 2t\\
z&=&4 &+& t
\enar\right.,\ t\in\R\]](Cours-IMG/166.png)
Exercice 9
Soit 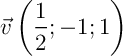 .
.
- Écrire une représentation paramétrique du plan
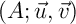
- Les points
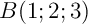 et
et 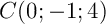 appartiennent-il à ce plan ?
appartiennent-il à ce plan ?
- Déterminer l'intersection
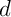 de ce plan et du plan
de ce plan et du plan
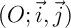 .
.
Préciser un point et un vecteur directeur de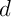 .
.
Produit scalaire dans l'espace
Voir aussi: