Devoir de maths corrigé, Systèmes d'équations, vecteurs et fonctions
seconde
Devoir de mathématiques, et corrigé, sur la résolution de systèmes d'équations, les vecteurs (vecteurs colinéaires et alignement de points), et la courbe d'une fonction posé en seconde générale, année scolaire 2024/2025
Exercice 1: Résoudre le système de deux équations
Résoudre le système: 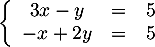
![\[\la\begin{array}{ccr} 3x-y&=&5\\ -x+2y&=&5 \enar\right.\]](/Generateur-Devoirs/2nde/Chap4/ex1.2_c/1.png)
On multiplie par 3 la deuxième équation pour obtenir le système équivalent
![\[\la\begin{array}{ccr} 3x-y&=&5\\ -3x+6y&=&15 \enar\right.\]](/Generateur-Devoirs/2nde/Chap4/ex1.2_c/2.png)
On ajoute alors les deux équations, ce qui nous donne
![\[5y=20\iff y=4\]](/Generateur-Devoirs/2nde/Chap4/ex1.2_c/3.png)
On peut alors substituer cette valeur dans la deuxième équation
![\[-x+2\tm4=5\iff x= 3\]](/Generateur-Devoirs/2nde/Chap4/ex1.2_c/4.png)
d'où la solution du système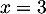 et
et 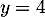 .
.
Cacher la correction
Correction exercice 1
On multiplie par 3 la deuxième équation pour obtenir le système équivalent
On ajoute alors les deux équations, ce qui nous donne
On peut alors substituer cette valeur dans la deuxième équation
d'où la solution du système
Cacher la correction
Exercice 2: Déterminer les coordonnées d'un point sur une droite
Soit 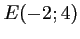 et
et 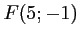 .
Déterminer l'ordonnée du point
.
Déterminer l'ordonnée du point 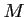 de la droite
de la droite 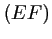 dont l'abscisse
est 2.
dont l'abscisse
est 2.
Soit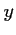 l'ordonnée du point
l'ordonnée du point 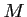 qui a donc pour coordonnées
qui a donc pour coordonnées 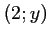 .
.
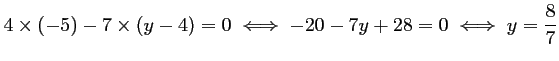
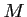 est donc
est donc
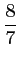 .
.
Cacher la correction
Correction exercice 2
Soit
![]() a pour coordonnées
a pour coordonnées
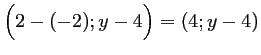 .
.
![]() a pour coordonnées
a pour coordonnées
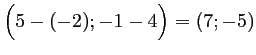 .
.
Le point ![]() appartient à la droite
appartient à la droite ![]() si et seulement si les
points
si et seulement si les
points ![]() ,
, ![]() et
et ![]() sont alignés, soit si et seulement si
sont alignés, soit si et seulement si
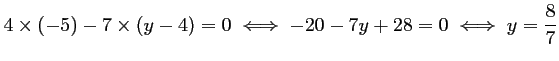
L'ordonnée du point
Cacher la correction
Exercice 3: Deux fonctions affines et des intersections
Soit 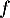 et
et 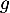 les fonctions
définies par les expressions
les fonctions
définies par les expressions
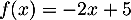 et
et
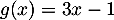 .
.
On note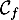 et
et 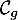 les courbes représentatives
de ces deux fonctions.
les courbes représentatives
de ces deux fonctions.
Cacher la correction
On note
- Déterminer les coordonnées du point
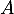 d'intersection
de
d'intersection
de 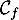 avec l'axe des ordonnées, et du point
avec l'axe des ordonnées, et du point
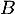 d'intersection de
d'intersection de 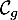 avec l'axe des abscisses.
avec l'axe des abscisses.
- Tracer
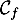 et
et 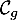 dans un repère.
dans un repère.
- Calculer les coordonnées du point d'intersection de
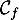 et
et 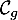 .
.
Correction exercice 3
- Soit
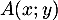 alors comme
alors comme 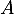 appartient à l'axe des ordonnées,
on a
appartient à l'axe des ordonnées,
on a 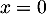 , et, comme
, et, comme 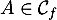 ,
, 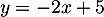 soit, avec
soit, avec 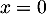 ,
,
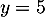 .
Ainsi on trouve
.
Ainsi on trouve 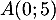 .
.
Soit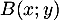 alors comme
alors comme 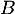 appartient à l'axe des abscisses,
on a
appartient à l'axe des abscisses,
on a 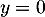 , puis comme
, puis comme 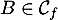 , on a
, on a 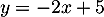 soit, avec
soit, avec 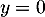 ,
,
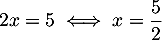 .
Ainsi, on trouve
.
Ainsi, on trouve 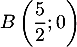 .
.
-
![\[\psset{unit=.7cm,arrowsize=7pt}
\begin{pspicture}(-1,-2)(4,5.5)
\psline{->}(-1.2,0)(4,0)
\psline{->}(0,-2)(0,6)
\multido{\i=-1+1}{7}{\psline(.1,\i)(-.1,\i)\rput(-.2,\i){\i}}
\multido{\i=-1+1}{5}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}}
\psplot{-.5}{3}{-2 x mul 5 add}\rput(2.5,.8){$\mathcal{C}_f$}
\psplot{-.3}{2}{3 x mul 1 sub}\rput(2.3,4.6){$\mathcal{C}_g$}
\end{pspicture}\]](/Generateur-Devoirs/2nde/Chap4/exFAI_c/17.png)
- Soit
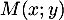 le point d'intersection de
le point d'intersection de 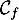 et
et  , alors on a
, alors on a
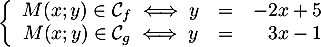
d'où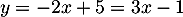 donc
donc
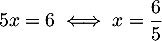 ,
et alors
,
et alors 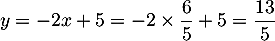 .
.
Ainsi, le point d'intersection est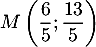 .
.
Cacher la correction
Exercice 4: Détermination de l'expression d'une fonction
|
On considère la fonction où On souhaite que la courbe représentative |
![$$(-2,1.)(2,8)
\psline[linewidth=1pt]{->}(-2.3,0)(3.5,0)
\psline[linewidth=1pt]{->}(0,-0.4)(0,8.5)
\rput(-0.3,-0.3){$O$}
\rput(1,-0.3){$1$}\rput(-0.15,1.25){$1$}
\multido{\i=-2+1}{6}{\psline[linewidth=0.4pt,linestyle=dashed](\i,-0.15)(\i,8.2)}
\multido{\i=1+1}{8}{\psline[linewidth=0.4pt,linestyle=dashed](-2.2,\i)(3.2,\i)}
\psplot[linewidth=1.3pt]{-1.5}{3.1}{x 2 exp -2 x mul add 3 add}
\rput(-1.65,7.5){$\mathcal{C}_f$}
\rput(-1,6){\Large $\tm$}\rput(-1.3,5.7){$A$}
\rput(1,2){\Large $\tm$}\rput(1.3,1.7){$B$}
$$](/Generateur-Devoirs/2nde/Chap4/ex3/12.png) |
Correction exercice 4
Le point
De même le point
En résumé, on a le système de deux équations:
En ajoutant les deux équations, on trouve
En soustrayant les deux équations, on trouve
En remplaçant finalement les valeurs trouvées pour
Cacher la correction
Quelques autres devoirs
calcul algébrique: calculs avec des puissance, factoriser des expressions algébriques, et résoudre des premières équations
sur la résolution d'équations (produit nul, quotient nul, équation avec un carré) et deux fractions avec des puissances à simplifier
sur quelques équations à résoudre, systèmes d'équations à deux inconnues, et la construction géométrique graphique de points et vecteurs
sur les vecteurs et coordonnées: calculs de coordonnées, et montrer l'alignement de points. Quelques équations et un système à résoudre
résolution de systèmes d'équations, les vecteurs (vecteurs colinéaires et alignement de points), et la courbe d'une fonction
Quelques exercices corrigés
Exercices corrigés
Factorisations
Exercices corrigés
3 équations du 1er degré
Exercices corrigés
Factorisation, développement et résolution d'équations
Exercices corrigés
Vérification de la solution d'une équation - Calcul sur les radicaux et fractions
Exercices corrigés
Vérification de la solution d'une équation - Calcul sur les radicaux et fractions
Voir aussi: