Sommes des termes de suites arithmétique et géométrique

Exercice corrigé - Spécialité maths, première générale

Énoncé

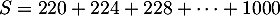
  1. Calculer la somme $S=220+224+228+\dots+1000$
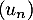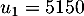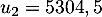  2. Soit $(u_n)$ une suite géométrique telle que $u_1=5150$ et $u_2=5304,5$.
    1. Déterminer la raison de cette suite ainsi que son premier terme $u_0$.
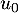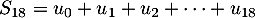    2. Soit $S_{18}=u_0+u_1+u_2+\dots+u_{18}$.
      Donner la valeur excate de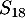 $S_{18}$ puis sa valeur approchée au centième.



Correction

Correction

  1. Il s'agit de la somme des termes consécutifs d'une suite arithmétique de raison 4,
    \[\begin{array}{ll} S&=220+224+228+\dots+1000\\ &=220+(220+4)+(220+2\tm4)+\dots+(220+195\tm4) \enar\]

    Il y a donc 196 termes dans cette somme, et donc
    \[\begin{array}{ll}S&=196\tm220+4(1+2+\dots+195)\\ &=196\tm220+4\tm\dfrac{195\tm196}2=119\,560\enar\]


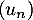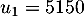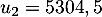  2. Soit $(u_n)$ une suite géométrique telle que $u_1=5150$ et $u_2=5304,5$.
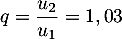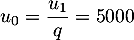    1. La raison de cette suite est $q=\dfrac{u_2}{u_1}=1,03$, et le premier terme est alors $u_0=\dfrac{u_1}q=5000$.

    2. \[\begin{array}{ll}S_{18}&=u_0+u_1+u_2+\dots+u_{18}\\[.5em] &=5000+5000\tm1,03+5000\tm1,03^2+\dots+5000\tm1,03^{18}\\[.5em] &=5000\bigl(1+1,03+1,03^2+\dots+1,03^{18}\bigr)\\[.5em] &=5000\dfrac{1-1,03^{19}}{1-1,03}\\[1.2em] &=5000\dfrac{1,03^{19}-1}{0,03}\\[1em] &\simeq125\,584,34\enar\]



Tag:Suites

Autres sujets au hasard: Lancer de dés


Voir aussi:

Quelques devoirs