Ensemble géométrique de points à déterminer
Exercice corrigé - Spécialité maths, première générale
Énoncé
- On note
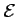 l'ensemble des points
l'ensemble des points 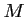 tels que:
tels que:
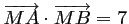 .
.
- a.
- Démontrer que
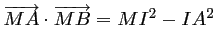 .
.
- b.
- En déduire que
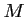 appartient à
appartient à
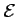 si et seulement
si:
si et seulement
si: 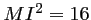 .
.
- c.
- Déterminer alors l'ensemble
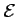 .
.
- On note
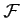 l'ensemble des points
l'ensemble des points 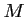 tels que:
tels que:
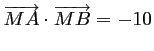 .
Déterminer l'ensemble
.
Déterminer l'ensemble
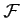 .
.
Correction
Correction
- a.
-
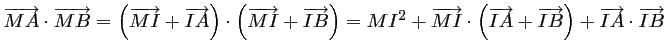
or,
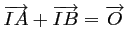 car
car 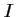 est le milieu de
est le milieu de ![$ [AB]$](/Generateur-Devoirs/1S/Chap6/ex3_c_img4.png) ,
et de même
,
et de même
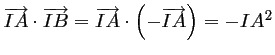 .
.
On a donc bien ainsi,
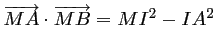 .
.
- b.
- On a alors,
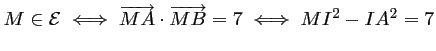 or,
or,
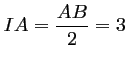 , d'où
, d'où 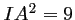 ,
et donc,
,
et donc,
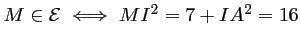 .
.
- c.
-
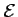 est donc le cercle de centre
est donc le cercle de centre 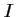 et de rayon
et de rayon
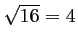 .
.
- En procédant comme précédemment, on a:
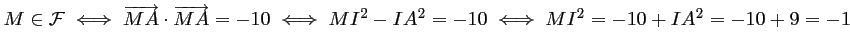 ce qui est impossible car pour tout point
ce qui est impossible car pour tout point 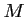 ,
,
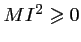 .
.
Ainsi l'ensemble
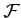 est vide:
est vide:
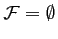 .
.
Tag:Produit scalaire
Voir aussi:
Quelques devoirs
Géométrie avec le produit scalaire, projeté orthogonal et calcul d'un angle et droites tangentes à une parabole perpendiculaires
Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
Probabilités conditionnelles et calculs de probabilités avec un arbre de probabilités. Propriétés algébriques de l'exponentielle et une étude de fonctionDevoir: Géométrie avec le produit scalaire, et probabilités conditionnelles et arbres de probabilités
une étude de fonction (calcul de dérivée et sens de variation) - Produit scalaire dans un repère: droites perpendiclaires et parallèles et calcul d'angle et distance d'un point à une droite en utilisant la projection orthogonale
une étude des variations d'une fonction - Calcul de la valeur approchée d'un angle avec le produit scalaire dans un repère - Probabilités conditionnelles et réunion / intersection d'événements
