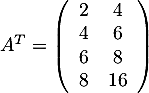Devoir de maths corrigé, Matrices et nombres complexes
Maths expertes, terminale générale
Devoir de mathématiques, et corrigé, posé en maths expertes, terminale générale, année scolaire 2023/2024
Exercice 1: Définition d'une matrice - Matrice Transposée
Soit 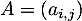 la matrice de dimension
la matrice de dimension 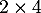 telle que
telle que 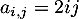 .
.
Écrire la matrice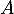 et sa transposée
et sa transposée 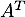 .
.
Écrire la matrice
Exercice 2: Puissance d'une matrice, par récurrence
Soit la matrice 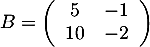 .
.
Montrer que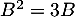 (détailler les calculs), puis en déduire
(détailler les calculs), puis en déduire 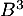 .
.
Donner alors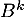 pour tout entier
pour tout entier 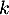 non nul (démontrer la formule, bien sûr).
non nul (démontrer la formule, bien sûr).
On calcule![$\begin{array}[t]{ll}
B^2&=\lp\begin{array}{cc}5&-1\\10&-2\enar\rp\,\lp\begin{array}{cc}5&-1\\10&-2\enar\rp\\[1em]
&=\lp\begin{array}{cc}5\tm5+(-1)\tm10&5\tm(-1)+(-1)\tm(-2)\\10\tm5+(-2)\tm10&10\tm(-1)+(-2)\tm(-2)\enar\rp\\[1em]
&=\lp\begin{array}{cc}15&3\\30&-6\enar\right)
=3B
\enar$](/Generateur-Devoirs/Mex/Matrices/expowrec_c/1.png)
On en déduit alors que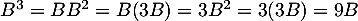 .
.
On a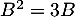 et
et 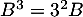 .
On peut conjecturer que
.
On peut conjecturer que 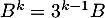 pour tout entier
pour tout entier 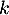 non nul.
non nul.
On le démontre par récurrence.
Initialisation: La propriété est vraie pour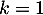 , car
, car 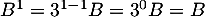 , et a même déjà été vérifiée pour
, et a même déjà été vérifiée pour 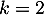 et
et 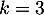 .
.
Hérédité: Supposons que pour un entier non nul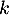 on ait
on ait 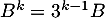 ,
,
alors on a
soit, en utilisant l'hypothèse de récurrence,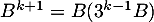
soit aussi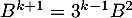 .
Or on a vu que
.
Or on a vu que 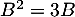 , et on obtient donc que
, et on obtient donc que
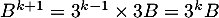 , ce qui montre que notre propriété est encore vraie au rang suivant
, ce qui montre que notre propriété est encore vraie au rang suivant 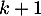 .
.
Conclusion: on vient de démontrer, d'après le principe de récurrence, que pour tout entier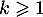 ,
, 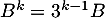 .
.
Cacher la correction
Montrer que
Donner alors
Correction exercice 2
On calcule
![$\begin{array}[t]{ll}
B^2&=\lp\begin{array}{cc}5&-1\\10&-2\enar\rp\,\lp\begin{array}{cc}5&-1\\10&-2\enar\rp\\[1em]
&=\lp\begin{array}{cc}5\tm5+(-1)\tm10&5\tm(-1)+(-1)\tm(-2)\\10\tm5+(-2)\tm10&10\tm(-1)+(-2)\tm(-2)\enar\rp\\[1em]
&=\lp\begin{array}{cc}15&3\\30&-6\enar\right)
=3B
\enar$](/Generateur-Devoirs/Mex/Matrices/expowrec_c/1.png)
On en déduit alors que
On a
On le démontre par récurrence.
Initialisation: La propriété est vraie pour
Hérédité: Supposons que pour un entier non nul
alors on a
soit, en utilisant l'hypothèse de récurrence,
soit aussi
Conclusion: on vient de démontrer, d'après le principe de récurrence, que pour tout entier
Cacher la correction
Exercice 3: Résolution d'une équation matricielle
Soit la matrice 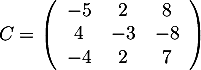 .
.
Soit la matrice
Cacher la correction
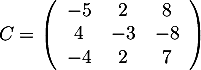 .
.
- Calculer
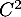 . Que peut-on alors dire de la matrice
. Que peut-on alors dire de la matrice 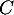 ?
?
- Déterminer la matrice
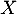 telle que
telle que
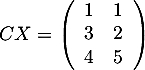
Correction exercice 3
Soit la matrice
-
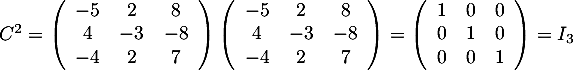 .
.
On en déduit que la matrice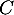 est inversible avec
est inversible avec 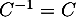 .
.
- En multipliant à gauche par
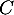 on obtient
on obtient
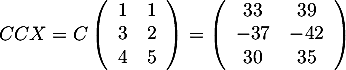 qui est aussi la matrice
qui est aussi la matrice 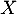 recherchée car
recherchée car
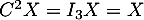
Cacher la correction
Exercice 4: Résolution matricielle d'un système 2x2
Soit le système 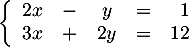
Écrire ce système sous forme matricielle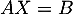 , en précisant les matrices
, en précisant les matrices 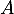 ,
, 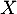 et
et 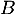 .
.
Résoudre alors matriciellement ce système.
Le système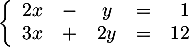 s'écrit sous la forme matricielle
s'écrit sous la forme matricielle 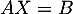 ,
avec les matrices
,
avec les matrices 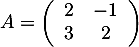 ,
, 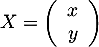 et
et 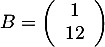 .
.
On connaît directement l'inverse de la matrice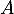 , soit
, soit
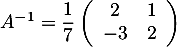
On résout alors le système matriciellement: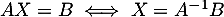 ,
soit
,
soit
![\[X=\dfrac17\lp\begin{array}{cc}2&1\\-3&2\enar\rp\lp\begin{array}{c}1\\12\enar\rp
=\lp\begin{array}{c}2\\3\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exsys_c/9.png)
Cacher la correction
Écrire ce système sous forme matricielle
Résoudre alors matriciellement ce système.
Correction exercice 4
Le système
On connaît directement l'inverse de la matrice
On résout alors le système matriciellement:
Cacher la correction
Exercice 5: Exercice complet sur les nombres complexes: 2nd degré, géométrie, formes algébriques et exponentielles
- Résoudre l'équation
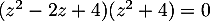 .
.
- On considère les points
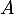 et
et 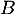 d'affixes respectives
d'affixes respectives
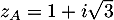 et
et 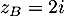 .
.
- Écrire
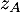 et
et 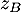 sous forme exponentielle et justifier que les points
sous forme exponentielle et justifier que les points 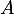 et
et 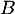 sont sur un cercle de centre
sont sur un cercle de centre  dont on précisera le rayon.
dont on précisera le rayon.
- Faire une figure et placer les points
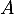 et
et 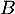 .
.
- Déterminer une mesure de l'angle
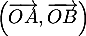 .
.
- Écrire
- On note
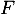 le milieu de
le milieu de ![$[AB]$](/Generateur-Devoirs/Mex/CplxPlan/excplt/15.png) .
.
- Placer le point
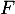 sur la figure précédente et calculer son affixe
sur la figure précédente et calculer son affixe 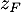 .
.
- Donner une mesure de l'angle
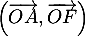 puis en déduire une mesure de l'angle
puis en déduire une mesure de l'angle 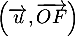 .
.
- Calculer le module de
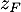 et en déduire l'écriture de
et en déduire l'écriture de 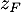 sous forme trigonométrique.
sous forme trigonométrique.
- En déduire la valeur exacte de:
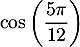
- Placer le point
Correction exercice 5
-
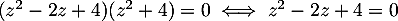 ou
ou 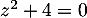
La première équation est du second degré, de discriminant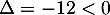 et admet donc deux racines complexes conjuguées:
et admet donc deux racines complexes conjuguées:
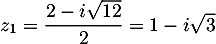 et
et
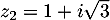 .
.
La deuxième équation est aussi du second degré, mais peut se résoudre plus simplement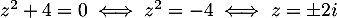 .
.
Ainsi, l'équation a quatre solutions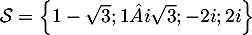 .
.
- On considère les points
 et
et  d'affixes respectives
d'affixes respectives
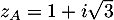 et
et 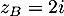 .
.
-
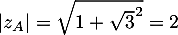 et donc
et donc
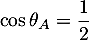 et
et 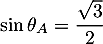 .
On en déduit que
.
On en déduit que 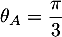 et donc que
et donc que
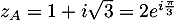 .
.
On a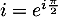 et donc
et donc 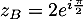 .
.
Comme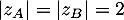 , on en déduit que les points
, on en déduit que les points 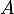 et
et 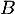 sont sur un cercle de centre
sont sur un cercle de centre  et de rayon 2.
et de rayon 2.
-
![\[\psset{unit=1cm,arrowsize=7pt}
\begin{pspicture}(-3,-2)(3,2)
\psline{->}(-2.6,0)(2.6,0)
\psline{->}(0,-2.6)(0,2.8)
\psline[linewidth=2pt]{->}(0,0)(1,0)\rput(.5,-.3){$\vec{u}$}
\multido{\i=-2+1}{5}{\psline[linestyle=dashed,linewidth=.3pt](\i,-2.2)(\i,2.6)
\rput(\i,-.2){$\i$}}
\multido{\i=-2+1}{5}{\psline[linestyle=dashed,linewidth=.3pt](-2.2,\i)(2.2,\i)
\rput[r](-.1,\i){$\i$}}
\psarc[linecolor=blue](0,0){2}{0}{360}
\rput(0,2){$\tm$}\rput(.2,2.3){$B$}
\rput(1,1.7){$\tm$}\rput(1.3,1.9){$A$}
\psline[linecolor=red,linewidth=1.5pt](0,2)(0,0)(1,1.7)(.5,1.85)(0,2)
\rput(0.5,1.85){$\tm$}\rput(.7,2){$F$}
\end{pspicture}\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/23.png)
- On a
![\[\begin{array}{ll}\lp\overrightarrow{OA},\overrightarrow{OB}\right)
&=\lp\vec{u},\overrightarrow{OB}\rp-\lp\vec{u},\overrightarrow{OB}\rp\\[.6em]
&=\arg(z_B)-\arg(z_A)\\[.6em]
&=\dfrac\pi2-\dfrac\pi3=\dfrac\pi6[2\pi]
\enar\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/24.png)
-
-
- On a
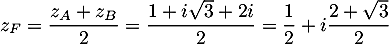
- Comme
 est un triangle isocèle en
est un triangle isocèle en  avec
avec  le milieu de
le milieu de ![$[AB]$](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/29.png) , on en déduit que
, on en déduit que 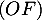 est aussi la bissectrice issue de
est aussi la bissectrice issue de  et donc que
et donc que
![\[\lp\overrightarrow{OA},\overrightarrow{OF}\rp=\dfrac12\lp\overrightarrow{OA},\overrightarrow{OB}\rp=\dfrac\pi{12}\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/32.png)
et ensuite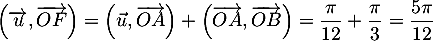 .
.
-
![\[|z_F|=\sqrt{\lp\dfrac12\rp^2+\lp\dfrac{2+\sqrt3}2\rp^2}
=\sqrt{\dfrac{1+(2+\sqrt3)^2}{4}}
=\sqrt{\dfrac{8+4\sqrt3}4}
=\sqrt{2+\sqrt3}
\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/34.png)
et connaissant l'argument de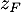 , on a alors trigonométrique:
, on a alors trigonométrique:
![\[z_F=\sqrt{2+\sqrt3}\lp\cos\lp\dfrac{5\pi}{12}\rp+i\sin\lp\dfrac{5\pi}{12}\rp\rp\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/36.png)
- En identifiant la partie réelle de
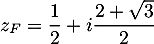 et celle de sa forme trigonométrique, on trouve que
et celle de sa forme trigonométrique, on trouve que
![\[\sqrt{2+\sqrt3}\cos\lp\dfrac{5\pi}{12}\rp=\dfrac12\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/38.png)
d'où
![\[\cos\lp\dfrac{5\pi}{12}\rp=\dfrac1{2\sqrt{2+\sqrt3}}\]](/Generateur-Devoirs/Mex/CplxPlan/excplt_c/39.png)
- On a
Cacher la correction
Quelques autres devoirs
sur les matrices et calcul matriciel, produit, puissance d'une matrice, définition de l'inverse d'une matrice
sur la factorisation et racines d'un polynôme complexe et matrices et calcul matriciel, diagonalisation et limites de suites
sur binôme de Newton et les racines de l'unité. Calcul de la puissance n-ième d'une matrice
sur les matrices, calcul matriciel et les nombres complexes: géométrie, formes algébriques et exponentielles.
Quelques exercices corrigés
Exercices corrigés
Ecrire sous forme algébrique
Exercices corrigés
Des équations complexes
Exercices corrigés
Une racine carrée complexe
Exercices corrigés
Une équation complexe
Exercices corrigés
Une équation complexe (bis)
Voir aussi: