Devoir de maths corrigé, Matrices
Maths expertes, terminale générale
Devoir de mathématiques, et corrigé, sur le calcul matriciel posé en maths expertes, terminale générale, année scolaire 2024/2025
Exercice 1: Calculs matriciels: additions et produits de matrices
On considère les matrices
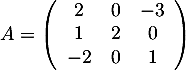 ,
,
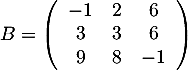 ,
,
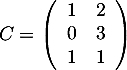 et
et
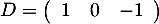
Calculer les matrices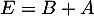 ,
, 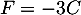 ,
, 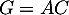 et
et 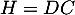
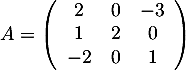 ,
,
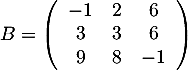 ,
,
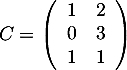 et
et
Calculer les matrices
Exercice 2: Puissances d'une matrice
Soit la matrice 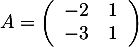 .
Calculer
.
Calculer 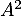 et
et 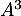 puis
puis 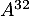 .
.
On calcule les produits définissant les puissances de la matrice
![\[A^2=\lp\begin{array}{cc}-2&1\\-3&1\enar\rp\lp\begin{array}{cc}-2&1\\-3&1\enar\rp
=\lp\begin{array}{cc}1&-1\\3&-2\enar\right)
\]](/Generateur-Devoirs/Mex/Matrices/expow_c/1.png)
et
![\[A^3
=\lp\begin{array}{cc}-2&1\\-3&1\enar\rp\lp\begin{array}{cc}1&-1\\3&-2\enar\rp
=\lp\begin{array}{cc}1&0\\0&1\enar\right)
\]](/Generateur-Devoirs/Mex/Matrices/expow_c/2.png)
On en déduit alors, en utilisant les règles de calcul sur les puissances,
![\[A^{32}=A^{3\tm10+2}=A^2\left( A^{10}\rp^3=A^2I^3=A^2\]](/Generateur-Devoirs/Mex/Matrices/expow_c/3.png)
Cacher la correction
Correction exercice 2
On calcule les produits définissant les puissances de la matrice
et
On en déduit alors, en utilisant les règles de calcul sur les puissances,
Cacher la correction
Exercice 3: Inverse d'une matrice
Soit la matrice 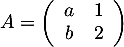 .
Déterminer les éventuelle valeurs des nombres réels
.
Déterminer les éventuelle valeurs des nombres réels 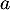 et
et 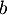 pour lesquels la matrice
pour lesquels la matrice 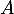 est inversible avec
est inversible avec 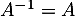 .
.
Donner alors cette matrice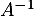 .
.
Si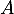 est inversible avec
est inversible avec 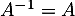 alors
alors
![\[AA^{-1}=A^2=I_2\]](/Generateur-Devoirs/Mex/Matrices/exinvcoeff_c/3.png)
On calcule le produit:
![\[A^2=\lp\begin{array}{cc}a&1\\b&2\enar\rp\lp\begin{array}{cc}a&1\\b&2\enar\rp
=\lp\begin{array}{cc}a^2+b&a+2\\ab+2b&b+4\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exinvcoeff_c/4.png)
Ainsi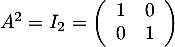 lorsque
lorsque
![\[\la\begin{array}{rcl}
a^2+b&=&1\\
a+2&=&0\\
ab+2b&=&0\\
b+4&=&1
\enar\right.\]](/Generateur-Devoirs/Mex/Matrices/exinvcoeff_c/6.png)
La 2ème et la 4ème équation donnent directement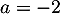 et
et 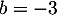 .
.
Comme on vérifie que ces valeurs conviennent aussi pour les deux autres équations:
![\[a^2+b=(-2)^2+(-3)=1\]](/Generateur-Devoirs/Mex/Matrices/exinvcoeff_c/9.png)
et
![\[ab+2b=-2(-3)+2(-3)=0\]](/Generateur-Devoirs/Mex/Matrices/exinvcoeff_c/10.png)
on en déduit que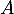 est bien inversible avec
est bien inversible avec 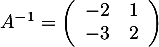 .
.
Cacher la correction
Donner alors cette matrice
Correction exercice 3
Si
On calcule le produit:
Ainsi
![\[\la\begin{array}{rcl}
a^2+b&=&1\\
a+2&=&0\\
ab+2b&=&0\\
b+4&=&1
\enar\right.\]](/Generateur-Devoirs/Mex/Matrices/exinvcoeff_c/6.png)
La 2ème et la 4ème équation donnent directement
Comme on vérifie que ces valeurs conviennent aussi pour les deux autres équations:
et
on en déduit que
Cacher la correction
Exercice 4: Matrices qui commutent
On suppose que
Correction exercice 4
En utilisant la définition de la matrice inverse
et on trouve donc que
On a donc ainsi bien trouvé que
Cacher la correction
Quelques autres devoirs
sur les matrices et calcul matriciel, produit, puissance d'une matrice, définition de l'inverse d'une matrice
sur la factorisation et racines d'un polynôme complexe et matrices et calcul matriciel, diagonalisation et limites de suites
sur binôme de Newton et les racines de l'unité. Calcul de la puissance n-ième d'une matrice
sur les matrices, calcul matriciel et les nombres complexes: géométrie, formes algébriques et exponentielles.
Quelques exercices corrigés
Exercices corrigés
Définition d'une matrice - Matrice Transposée
Exercices corrigés
Calculs matriciels: additions et produits de matrices
Exercices corrigés
Inverse d'une matrice avec des paramètres
Exercices corrigés
Matrices qui commutent
Exercices corrigés
Résolution d'une équation matricielle
Voir aussi:
![\[E=B+A=\lp\begin{array}{ccc}1&2&3\\4&5&6\\7&8&0\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/excalc_c/1.png)
![\[F=\lp\begin{array}{cc}-3&-6\\0&-9\\-3&-3\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/excalc_c/2.png)
![\[G=\lp\begin{array}{ccc}2&0&-3\\1&2&0\\-2&0&1\enar\rp\lp\begin{array}{cc}1&2\\0&3\\1&1\enar\rp
=\lp\begin{array}{cc}-1&1\\1&8\\-1&-3\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/excalc_c/3.png)
![\[H=\lp\begin{array}{ccc}1&0&-1\enar\rp\lp\begin{array}{cc}1&2\\0&3\\1&1\enar\rp
=\lp\begin{array}{cc}0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/excalc_c/4.png)