Une équation complexe
Exercice corrigé - Maths expertes, terminale générale
Énoncé
Résoudre 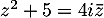
Correction
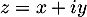 , avec
, avec 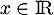 et
et 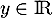 , et alors l'équation
, et alors l'équation
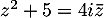 est équivalente à
est équivalente à
![\[\begin{array}{ll}&(x+iy)^2+5=4i(x-iy)\\[.5em]
\iff& \left( x^2-y^2+5\right) +2ixy=4y+4ix
\enar\]](/Generateur-Devoirs/TS/ChapComplexes/exeq_c/5.png)
et donc, en identifiant les parties réelles et imaginaires, l'équation est équivalente au système
![\[\la\begin{array}{rcr}
x^2-y^2+5&=&4y\\
2xy&=&4x
\enar\right.\]](/Generateur-Devoirs/TS/ChapComplexes/exeq_c/6.png)
La 2ème équation donne
![\[2xy-4x=2x(y-2)=0\]](/Generateur-Devoirs/TS/ChapComplexes/exeq_c/7.png)
soit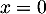 ou
ou 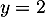 .
.
Si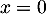 , la 1ère équation du système devient
, la 1ère équation du système devient
![\[-y^2+5=4y\iff y^2+4y-5=0\]](/Generateur-Devoirs/TS/ChapComplexes/exeq_c/11.png)
qui est une équation du second degré de discriminant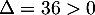 et qui admet donc deux solutions réelles distinctes
et qui admet donc deux solutions réelles distinctes 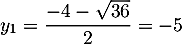 et
et 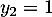 .
.
Si , alors la 1ère équation du système devient
, alors la 1ère équation du système devient
![\[x^2-4+5=8 \iff x^2=7\iff x=\pm\sqrt7\]](/Generateur-Devoirs/TS/ChapComplexes/exeq_c/16.png)
L'équation de départ admet donc quatre solutions:
![\[\mathcal{S}=\Bigl\{i \,; -5i\,; \sqrt7+2i\,; \sqrt7-2i \Bigr\}\]](/Generateur-Devoirs/TS/ChapComplexes/exeq_c/17.png)
Correction
On pose![\[\begin{array}{ll}&(x+iy)^2+5=4i(x-iy)\\[.5em]
\iff& \left( x^2-y^2+5\right) +2ixy=4y+4ix
\enar\]](/Generateur-Devoirs/TS/ChapComplexes/exeq_c/5.png)
et donc, en identifiant les parties réelles et imaginaires, l'équation est équivalente au système
La 2ème équation donne
soit
Si
qui est une équation du second degré de discriminant
Si
L'équation de départ admet donc quatre solutions:
Tag:Nombres Complexes - Algébrique
Voir aussi:
Quelques devoirs
sur les nombres complexes: forme algébrique des nombres complexes et résolution d'équations complexes
sur les nombres complexes: résolution d'équations et forme algébrique. Arithmétique, divisibilité et division euclidienne
sur les nombres complexes, point de vue algébrique. Calculs algébriques sur les nombres complexes, inverse d'un nombre complexe et résolution d'équations
sur les nombres complexes et polynômes. Résolution d'une éuqation complexe. Racine d'un polynôme et factorisation du polynôme. Quotients et restes de division euclidienne. Divisiblité par 8
