Devoir de maths corrigé, Polynômes et matrices
Maths expertes, terminale générale
Devoir de mathématiques, et corrigé, sur les matrices et factorisation des polynôme posé en maths expertes, terminale générale, année scolaire 2024/2025
Exercice 1: Factorisation et racines d'un polynôme complexe
On considère le polynôme 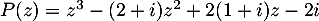
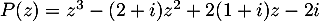
Cacher la correction
- Calculer
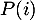 et en déduire une factorisation de
et en déduire une factorisation de 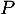 .
.
- Calculer toutes les racines de
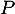 .
.
Correction exercice 1
- On a
![\[\begin{array}{ll}P(i)&=i^3-(2+i)i^2+2(1+i)i-2i\\
&=-i+(2+i)+2i-2-2i\\
&=0
\enar\]](/Generateur-Devoirs/Mex/CplxPol/exPol3_c/2.png)
ce qui signifie que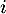 est une racine du polynôme
est une racine du polynôme 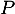 et donc que celui-ci se factorise par
et donc que celui-ci se factorise par 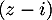 , c'est-à-dire
, c'est-à-dire
![\[P(z)=(z-i)Q(z)\]](/Generateur-Devoirs/Mex/CplxPol/exPol3_c/6.png)
Le polynôme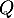 est ici de degré au plus 2, et on peut le déterminer par identification ou avec une division euclidienne.
est ici de degré au plus 2, et on peut le déterminer par identification ou avec une division euclidienne.
Division euclidienne:
![\[\begin{array}{ll}z^3-(2+i)z^2+2(1+i)z-2i &\psline(-.1,.3)(-.1,-3.6) z-i\\
z^3-iz^2 &\psline(0,.4)(2,.4) z^2-2z+2 \\[.4em]
\psline(0,.5)(2.5,.5)
\hspace*{3.8em}-2z^2+2(1+i)z\\
\hspace*{3.8em}-2z^2+2iz\\[.4em]
\psline(1.4,.5)(4.5,.5)
\hspace*{10.2em}2z-2i\\
\hspace*{10.2em}2z-2i\\[.4em]
\psline(4,.5)(5.6,.5)
\hspace*{12.6em}0\enar\]](/Generateur-Devoirs/Mex/CplxPol/exPol3_c/8.png)
ce qui nous donne donc la factorisation
![\[P(z)=(z-i)(z^2-2z+2)\]](/Generateur-Devoirs/Mex/CplxPol/exPol3_c/9.png)
Identification: Comme le polynôme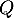 recherché est de degré 2, il s'écrit sous la forme
recherché est de degré 2, il s'écrit sous la forme 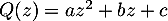 et il reste à déterminer ses trois coefficients.
et il reste à déterminer ses trois coefficients.
On développe la factorisation recherchée:
![\[\begin{array}{ll}P(z)&=(z-i)(az^2+bz+c)\\
&=az^3+(b-ai)z^2+(c-bi)z-ci
\enar\]](/Generateur-Devoirs/Mex/CplxPol/exPol3_c/12.png)
et comme il s'agit toujours du même polynôme
![\[P(z)=z^3-(2+i)z^2+2(1+i)z-2i\]](/Generateur-Devoirs/Mex/CplxPol/exPol3_c/13.png)
on identifie les coefficients
![\[\la\begin{array}{ll}a=1\\
b-ai=-(2+i)\\
c-bi=2(1+i)\\
-ci=-2i\enar\right.\]](/Generateur-Devoirs/Mex/CplxPol/exPol3_c/14.png)
ce qui nous donne les coefficients:
![\[\la\begin{array}{ll}
a&=1\\
b&=-2\\
c&=2
\enar\right.\]](/Generateur-Devoirs/Mex/CplxPol/exPol3_c/15.png)
et on a donc trouvé la factorisation
![\[P(z)=(z-i)(z^2-2z+2)\]](/Generateur-Devoirs/Mex/CplxPol/exPol3_c/16.png)
- On cherche alors toutes les racines de
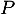 , c'est-à-dire les solutions de l'équation
, c'est-à-dire les solutions de l'équation 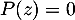 , soit, pour le produit nul,
, soit, pour le produit nul,
![\[z-i=0\iff z=i\]](/Generateur-Devoirs/Mex/CplxPol/exPol3_c/19.png)
soit
![\[z^2-2z+2=0\]](/Generateur-Devoirs/Mex/CplxPol/exPol3_c/20.png)
Cette équation du second degré a pour discriminant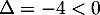 et admet donc deux racines complexes conjuguées,
et admet donc deux racines complexes conjuguées,
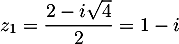 et
et 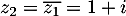 .
.
En résumé, le polynôme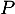 admet trois racines
admet trois racines 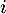 ,
, 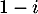 et
et 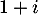 .
.
Cacher la correction
Exercice 2: Déterminant d'une matrice et théorème de Cayley-Hamilton
Soit la matrice 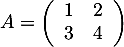 .
.
Pour tout nombre réel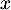 , on pose
, on pose 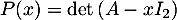 , où
, où 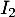 est la matrice identité d'ordre 2.
est la matrice identité d'ordre 2.
On a
![\[\begin{array}{ll}A - xI_2&=\lp\begin{array}{cc}1&2\\3&4\enar\rp-x\lp\begin{array}{cc}1&0\\0&1\enar\rp\\[1.4em]
&=\lp\begin{array}{cc}1-x&2\\3&4-x\enar\rp\enar\]](/Generateur-Devoirs/Mex/Matrices/exCayley_c/1.png)
et donc
![\[\begin{array}{ll}P(x)&=\det(A - xI_2)\\[.5em]
&=(1-x)(4-x)-6\\[.5em]
&=x^2-5x-2\enar\]](/Generateur-Devoirs/Mex/Matrices/exCayley_c/2.png)
On calcule ensuite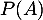 :
:
![\[P(A)=A^2-5A-2I_2\]](/Generateur-Devoirs/Mex/Matrices/exCayley_c/4.png)
avec
![\[A^2=\lp\begin{array}{cc}1&2\\3&4\enar\rp\lp\begin{array}{cc}1&2\\3&4\enar\rp=
\lp\begin{array}{cc}7&10\\15&22\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exCayley_c/5.png)
d'où
![\[P(A)=\lp\begin{array}{cc}7&10\\15&22\enar\rp-5\lp\begin{array}{cc}1&2\\3&4\enar\rp-2\lp\begin{array}{cc}1&0\\0&1\enar\rp
\]](/Generateur-Devoirs/Mex/Matrices/exCayley_c/6.png)
et on trouve finalemnt la matrice nulle:
![\[P(A)=\lp\begin{array}{cc}0&0\\0&0\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exCayley_c/7.png)
Remarque: le polynôme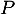 s'appelle le polynôme caractéristique de la matrice
s'appelle le polynôme caractéristique de la matrice 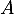 , et la propriété
, et la propriété 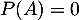 est le théorème de Cayley-Hamilton
est le théorème de Cayley-Hamilton
Cacher la correction
Pour tout nombre réel
- Donner l'expression de
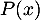 .
.
- Pour un polynôme
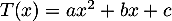 on associe le polynôme matriciel
on associe le polynôme matriciel 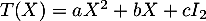 pour toute matrice carrée
pour toute matrice carrée 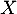 .
.
Calculer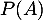 .
.
Correction exercice 2
On a
![\[\begin{array}{ll}A - xI_2&=\lp\begin{array}{cc}1&2\\3&4\enar\rp-x\lp\begin{array}{cc}1&0\\0&1\enar\rp\\[1.4em]
&=\lp\begin{array}{cc}1-x&2\\3&4-x\enar\rp\enar\]](/Generateur-Devoirs/Mex/Matrices/exCayley_c/1.png)
et donc
![\[\begin{array}{ll}P(x)&=\det(A - xI_2)\\[.5em]
&=(1-x)(4-x)-6\\[.5em]
&=x^2-5x-2\enar\]](/Generateur-Devoirs/Mex/Matrices/exCayley_c/2.png)
On calcule ensuite
avec
d'où
et on trouve finalemnt la matrice nulle:
Remarque: le polynôme
Cacher la correction
Exercice 3: Diagonalisation d'une matrice et limites de suites
On considère les matrices ![$A=\lp\begin{array}{cc}\dfrac13&0\\[1em]-\dfrac13&1\enar\rp$](/Generateur-Devoirs/Mex/Matrices/exdiaglim/1.png) et
et 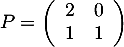 .
.
Cacher la correction
![$A=\lp\begin{array}{cc}\dfrac13&0\\[1em]-\dfrac13&1\enar\rp$](/Generateur-Devoirs/Mex/Matrices/exdiaglim/1.png) et
et - Montrer que
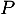 est inversible et donner sa matrice inverse
est inversible et donner sa matrice inverse 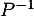 .
.
- Calculer la matrice
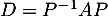 .
.
- Calculer
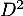 ,
, 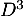 puis donner
puis donner 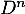 (sans justification supplémentaire).
(sans justification supplémentaire).
- Donner l'expression de
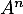 en fonction de
en fonction de 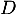 et
et 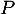 .
.
- On note
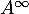 et
et 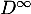 les matrices limites des matrices
les matrices limites des matrices 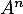 et
et 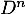 , c'est-à-dire
, c'est-à-dire
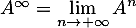 et
et
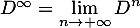 .
.
Déterminer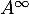 .
.
- On définit les suites
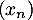 et
et 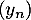 par
par 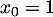 et
et 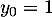 puis par
les relations de récurrence
puis par
les relations de récurrence
![\[\la\begin{array}{ll}x_{n+1}&=\dfrac13x_n\\[.9em]y_{n+1}&=-\dfrac13x_n+y_n\enar\right.\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim/23.png)
Déterminer les limites de ces deux suites.
Correction exercice 3
- On a
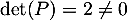 et donc
et donc 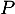 est bien inversible, d'inverse
est bien inversible, d'inverse
![\[P^{-1}=\dfrac12\lp\begin{array}{cc}1&0\\-1&2\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/3.png)
- On calcule les deux produits, successivement,
![\[\begin{array}{ll}D&=P^{-1}AP\\
&=\dfrac12\lp\begin{array}{cc}1&0\\-1&2\enar\right)
\lp\begin{array}{cc}\dfrac13&0\\[1em]-\dfrac13&1\enar\right) P\\[2em]
&=\dfrac12\lp\begin{array}{cc}\dfrac13&0\\[1em]-1&2\enar\rp\lp\begin{array}{cc}2&0\\1&1\enar\rp\\[2em]
&=\dfrac12\lp\begin{array}{cc}\dfrac23&0\\[1em]0&2\enar\right)
\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/4.png)
et on trouve donc la matrice diagonale![$D=\lp\begin{array}{cc}\dfrac13&0\\[1em]0&1\enar\rp$](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/5.png)
- On calcule facilement que
![\[D^2=\lp\begin{array}{cc}\lp\dfrac13\rp^2&0\\[1em]0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/6.png)
et
![\[D^3=\lp\begin{array}{cc}\lp\dfrac13\rp^3&0\\[1em]0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/7.png)
qu'on généralise à
![\[D^n=\lp\begin{array}{cc}\lp\dfrac13\rp^n&0\\[1em]0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/8.png)
- On a la relation
![\[D=P^{-1}AP \iff PDP^{-1}=A\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/9.png)
et alors
![\[\begin{array}{ll}A^n&=\underbrace{A\,A\,A\,\dots\,A}_{n \text{termes}}\\[1.6em]
&=PA\underbrace{P^{-1}P}_{=I_2}D\underbrace{P^{-1}P}_{=I_2}DP{-1}\dots\,\underbrace{P^{-1}P}_{=I_2}DP^{-1}\\[1.6em]
&=PD^nP^{-1}
\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/10.png)
- Comme
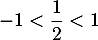 , on a
, on a 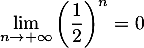 et donc
et donc
![\[D^\infty=\lp\begin{array}{cc}0&0\\0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/13.png)
et alors, en passant à la limite dans les produits
![\[\begin{array}{ll}A^\infty&=PD^\infty P^{-1}\\
&=\lp\begin{array}{cc}2&0\\1&1\enar\rp\lp\begin{array}{cc}0&0\\0&1\enar\rp P^{-1}\\[1.2em]
&=\lp\begin{array}{cc}0&0\\0&1\enar\rp\dfrac12\lp\begin{array}{cc}1&0\\-1&2\enar\rp\\[1.2em]
&=\dfrac12\lp\begin{array}{cc}0&0\\-1&2\enar\rp\\[1.2em]
&=\lp\begin{array}{cc}0&0\\-\dfrac12&1\enar\right)
\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/14.png)
- On pose
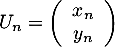 , et alors on a
, et alors on a
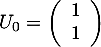 et les relations de récurrence s'écrivent matriciellement
et les relations de récurrence s'écrivent matriciellement
![\[U_{n+1}=AU_n\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/17.png)
Il s'agit donc d'une suite géométrique, et on a directement pour tout entier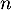 ,
,
![\[U_n=A^nU_0\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/19.png)
et, avec les calculs précédents, on trouve la limite
![\[\begin{array}{ll}\dsp\lim_{n\to+\infty}U_n&=D^\infty U_0\\
&=\lp\begin{array}{cc}0&0\\-\dfrac12&1\enar\rp\lp\begin{array}{c}1\\1\enar\rp\\[1.5em]
&=\lp\begin{array}{c}0\\\dfrac12\enar\right)
\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/20.png)
c'est-à-dire, en revenant aux suites de l'énoncé,
![\[\begin{array}{ll}\dsp\lim_{n\to+\infty}x_n=0\\\dsp\lim_{n\to+\infty}y_n=\dfrac12\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiaglim_c/21.png)
Cacher la correction
Quelques autres devoirs
sur les matrices et calcul matriciel, produit, puissance d'une matrice, définition de l'inverse d'une matrice
sur la factorisation et racines d'un polynôme complexe et matrices et calcul matriciel, diagonalisation et limites de suites
sur binôme de Newton et les racines de l'unité. Calcul de la puissance n-ième d'une matrice
sur les nombres complexes et polynômes. Résolution d'une éuqation complexe. Racine d'un polynôme et factorisation du polynôme. Quotients et restes de division euclidienne. Divisiblité par 8
d'arithmétique (division euclidienne et congruences) et factorisation des polynômes complexes.
Quelques exercices corrigés
Exercices corrigés
Définition d'une matrice - Matrice Transposée
Exercices corrigés
Calculs matriciels: additions et produits de matrices
Exercices corrigés
Inverse d'une matrice avec des paramètres
Exercices corrigés
Matrices qui commutent
Exercices corrigés
Résolution d'une équation matricielle
Voir aussi: