Géométrie dans l'espace
Trois exercices complets pour finir ("d'après Bac")
Exercice 24 (D'après Bac 2003)
L'espace est rapporté à un repère orthonormal
- Montrer que le triangle
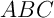 est un triangle rectangle.
est un triangle rectangle.
- Montrer que la droite
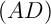 est perpendiculaire au plan
est perpendiculaire au plan 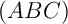 .
.
- Calculer le volume du trétraèdre
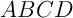 .
.
- Montrer que l'angle géométrique
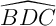 a pour mesure
a pour mesure 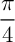 en radians.
en radians.
Exercice 25 (D'après Bac 2005)
Partie A. Soit Démontrer que le plan médiateur de
Partie B. Dans un RON, on considère les points
Démontrer que le plan médiateur de
Exercice 26
- Donner une équation de la sphère
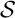 .
. -
- Quelles sont les coordonnées des points
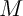 et
et 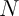 ?
? - Déterminer une représentation paramétrique de la droite
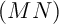 .
.
- Quelles sont les coordonnées des points
- Montrer que la droite
 est tangente à la sphère
est tangente à la sphère
 si, et seulement si,
si, et seulement si, 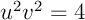 .
.
Voir aussi: