Devoir de maths corrigé, Equations, taux d'évolution et fonctions

seconde

Devoir de mathématiques, et corrigé, sur les pourcentages (évolution et taux global), sur les fonctions (graphique, courbe et inéquation) et la résolution d'inéquations (tableaux de signes), posé en seconde générale, année scolaire 2023/2024

Exercice 1: Résolution d'inéquations

Résoudre les inéquations:

Correction exercice 1

$\begin{array}{ll} &(I_1): (2x+3)(x-5)\leqslant (2x-4)(2x+3)\\[0.2cm] &\iff (2x+3)(x-5)- (2x-4)(2x+3)\leqslant0 \\[0.2cm] &\iff (2x+3)(-x-1)\leqslant0 \end{array} \begin{tabular}{|c|p{.6em}cccccr|}\hline $x$ & $-\infty$ && $-\frac32$ && $-1$ && $+\infty$ \\\hline $2x+3$& & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$& \\\hline $-x-1$& & $+$ & $|$ & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$& \\\hline $(2x+3)(-x-1)$ & & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$& \\\hline \end{tabular}$

$\text{Les solutions de } (I_1) \text{ sont donc: } \mathcal{S}=\Bigl]-\infty;-\dfrac32\Bigr]\cup\Bigl[-1;+\infty\Bigr[$

$\begin{array}{ll} (I_2): \dfrac{3x+2}{2x+5}\geqslant \dfrac12 %\\[0.3cm] &\iff \dfrac{3x+2}{2x+5}- \dfrac12 \geqslant0\\[0.3cm] &\iff \dfrac{4x-1}{2(2x+5)} \geqslant0\\[0.3cm] \enar\qquad \begin{tabular}{|c|p{.6em}cccccr|}\hline $x$ & $-\infty$ && $-\frac52$ && $\frac14$ && $+\infty$ \\\hline $4x-1$& & $-$ & $|$ & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$& \\\hline $2x+5$& & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$& \\\hline $\dfrac{4x-1}{2(2x+5)}$ & & $+$ & \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$& \\\hline \end{tabular}$

$\text{Les solutions de } (I_2) \text{ sont donc: } \mathcal{S}=\Bigl]-\infty;-\dfrac52\Bigr[\cup\Bigl[\dfrac14;+\infty\Bigr]$

Cacher la correction

Exercice 2: Pourcentages divers - Pourcentage global de remise, d'augmentation

Les questions suivantes sont indépendantes.

Dans une assemblée, on compte 66 femmes et 37 hommes. Calculer le pourcentage d'hommes dans cette assemblée.
Un produit alimentaire de 326g contient 35,6% de lipides. Quelle est la masse de lipides ?
Durant la première semaine des soldes, un magasin propose 40% de remise sur tous les articles. Lors de la seconde semaine, le magasin propose 20% de remise supplémentaire sur tous les articles non vendus.
Combien coûte finalement un article qui valait initialement 150 euros ?
Quel est le pourcentage de la remise globale ?
Le prix du pain augmente de 2% chaque année. Chez mon boulanger, une baguette de pain coûte actuellement 1,50 euros.
Combien coûtera-t-elle dans deux ans ? dans 10 ans ? dans 30 ans ?

Correction exercice 2

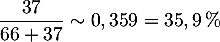Le pourcentage (ou proportion) d'hommes dans l'assemblée est $\dsp\frac{37}{66+37}\sim 0,359 = 35,9\,\%$ .
La masse de lipides est : 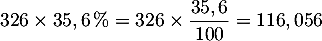$\displaystyle 326\times 35,6\,\%=326\times\frac{35,6}{100}=116,056$ g.
L'article coûte finalement 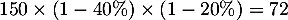$150\tm(1-40\%)\tm(1-20\%)=72$ euros.
Le prix a été multiplié par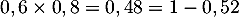 $0,6\tm0,8=0,48=1-0,52$ , soit un pourcantage de global de remise de 52%.
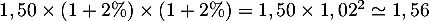
Dans deux ans, la baguette vaudra $1,50\tm(1+2\%)\tm(1+2\%)=1,50\tm1,02^2\simeq1,56$
Dans 10 ans, elle coûtera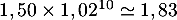 $1,50\tm1,02^{10}\simeq1,83$
Dans 30 ans, elle coûtera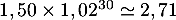 $1,50\tm1,02^{30}\simeq2,71$

Cacher la correction

Exercice 3: Fonction: variation, courbe et inéquations graphiques et algébriques

Monsieur Dupré, PDG d'une société fabriquant du mobilier urbain, s'intéresse au bénéfice réalisé par sa société.
Il fabrique et vend, par semaine,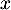

lots de mobilier.
Le coût unitaire de production, en euros,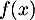

(coût de production pour un lot de mobilier) s'exprime en fonction du nombre de lots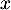

par l'expression:

.
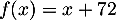A ce coût unitaire s'ajoute des frais de fonctionnement de l'usine de production s'élevant à 3 952 euros par semaine, quelle que soit la quantité de lots produite.

Chaque lot est vendu 200 euros. Montrer que le bénéfice réalisé pour 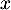lots produits et vendus est:

$B(x)=-x^2+128x-3952$
Montrer que pour tout nombre réel 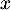, on a 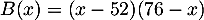. Déterminer alors le nombre de lots que doit produire et fabriquer la société pour être rentable (pour avoir un bénéfice positif …).
Montrer que .
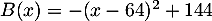Etudier alors les variations de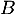 sur .
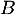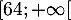On admet pour la suite que la fonction est décroissante sur $[64;+\infty[$ .
Dresser le tableau de variations de .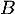
Quel est le bénéfice maximal que peut espérer Monsieur Dupré ? Pour combien de lots fabriqués et vendus ?

Correction exercice 3

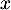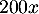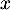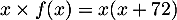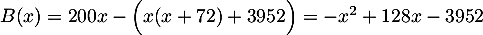lots produits et vendus rapportent euros. La production de ces lots coûtent $x\times f(x)=x(x+72)$ euros plus 3952 euros. Ainsi, le bénéfice est $B(x)=200x - \Big( x(x+72)+3952\Big)=-x^2+128x-3952$ .
En développant, on a 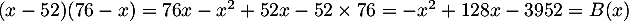$(x-52)(76-x)=76x-x^2+52x-52\tm76=-x^2+128x-3952=B(x)$ . Ainsi, le bénéfice pour 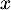lots produits et vendus est .

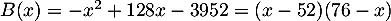$\begin{tabular}[t]{|c|ccccccc|}\hline $x$&$-\infty$ & & $52$ & & $76$ & & $+\infty$ \\\hline $x-52$ & & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ &\\\hline $76-x$ & & $+$ & $|$ & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline $B(x)$& & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline \end{tabular}$

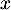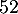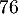La société est rentable lorsque le bénéfice est positif, soit donc lorsque le nombre de lots produits et vendus est compris entre et lots.
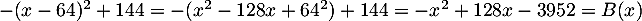. Ainsi, pour tout , .

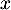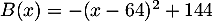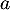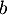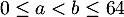Soit et deux nombres quelconques de tels que $0\leq a< b\leq 64$ ,

alors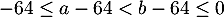 $-64\leq a-64<b-64\leq 0$ ,
donc,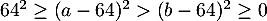 $64^2\geq (a-64)^2>(b-64)^2\geq 0$ , en élevant au carré des nombres négatifs,
d'où,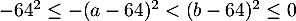 $-64^2\leq -(a-64)^2<(b-64)^2\leq 0$ , en multipliant par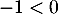
soit,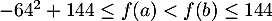 $-64^2+144\leq f(a)<f(b)\leq 144$

donc,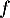 est croissante sur

$\begin{tabular}{|c|ccccc|}\hline $x$ & $0$ & & $64$ & & $+\infty$ \\\hline & & & $144$ &&\\ $B(x)$ & & \Large{$\nearrow$}& &\Large{$\searrow$}& \\ & $-3952$ & &&&\\\hline \end{tabular}$
Le bénéfice maximum que peut espérer M. Duspré est de 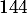euros, pour 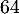lots produits et vendus. (remarque: pour 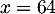lots la société est bien rentable, cf. question 1)).